Con la classe 2B₂ della Scuola secondaria di Primo Grado dell’IC AM Ricci di Rieti abbiamo sperimentato un percorso culturale che ha permesso a me e ai ragazzi di riflettere su tematiche di scienze, matematica e storia. Come in altre nostre avventure ci ha guidato il Liber Abaci di Leonardo Fibonacci.

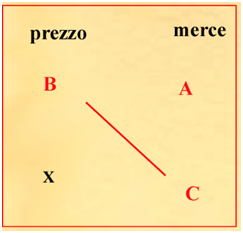
Abbiamo considerato ed analizzato alcune delle molte relazioni lineari riportate in questo libro e che permettono di risolvere una grande quantità di problemi, anche apparentemente diversi tra loro, alcuni molto realistici e comprensibili dai ragazzi. Fibonacci descrive una sorta di algoritmo visivo che, una volta compresa e verificata l’ipotesi di proporzionalità diretta, ossia di linearità, esistente tra le grandezze che compaiono in un problema, serve ad aiutare la memoria fissando i dati del problema e indicando la procedura per trovare la soluzione. Se P è una relazione di proporzionalità diretta tra una grandezza a e la grandezza corrispondente P(a), come al esempio il prezzo P(a) di una data merce a, allora

e quest’ultima relazione, noti 3 dei 4 numeri proporzionali, permette di calcolare il quarto numero eseguendo l’operazione inversa della moltiplicazione. Scritti i dati in una tabella come nella figura, in rosso i dati noti , l’algoritmo consiste nel moltiplicare i numeri sulla diagonale (B per C ) e dividere per il numero restante A

.
La regola del tre: A=quantità di una merce B=prezzo di A, C=una seconda quantità della stessa merce; A, B, C sono noti, X=

B

C

A è il prezzo della quantità C
Le grandezze su cui lavora Fibonacci sono di tipo diverso, ma molto frequenti sono i problemi in cui egli si occupa di prezzi della merce che variano in funzione delle unità di misura, problema molto importante per l’economia del tempo, quando vi erano molte unità di misura diverse in regioni anche contigue.
Altro tipo di problema affrontato è quello del cambio delle monete di diverso valore, per una ragione evidentemente analoga alla precedente; non ultimo quello relativo alla quantità di metallo prezioso presente nelle monete, una volta che se ne conosca la concentrazione.
Si tenga presente, nella lettura di quanto segue, che per Fibonacci non esistono frazioni improprie ed egli scrive solo “rotti” e “sani”, quindi le frazioni improprie vengono rappresentate con dei numeri misti. Nel testo io scriverò nel numero misto prima la parte intera e poi la rotta, al contrario di ciò che faceva Fibonacci che scriveva i numeri alla maniera araba, da destra a sinistra, prima la rotta seguita dalla mista senza segno di addizione, come usiamo far oggi. Così

1

25 di Fibonacci sta per 5+

1

2 =

11

2.

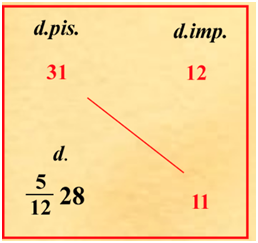
Il problema riportato nella seguente figura è relativo al cambio tra soldi imperiali e denari pisanini e corrisponde al seguente:

Agli studenti viene fatto leggere il testo del problema dall’originale e viene proposto di realizzare lo schema dell’algoritmo di Fibonacci, di cui viene data la soluzione in seguito.

Sulla carta abbiamo risolto problemi analoghi al precedente, andando a notare come questa schematizzazione permette di farlo in maniera diretta senza uno studio sistematico e mnemonico delle proporzioni e delle loro proprietà, anzi costruendo dei primordiali prerequisiti del calcolo matriciale.

Ispirandosi a tale attività, inoltre la classe 2 B₂ ha studiato le proporzioni nell’ambiente del laboratorio scientifico attraverso la preparazione di diverse quantità di soluzioni acquose e colorante alimentare che presentino tutte la stessa intensità di colorazione quindi la stessa concentrazione in colorante, ed in seguito in sale . La realizzazione di una soluzione a concentrazione costante di un soluto ad alta solubilità sotto la soglia di saturazione è un esempio di linearità tra grammi di soluto e volume di soluzione.

In seguito il nostro interesse si è spostato su un argomento multidisciplinare. Il mondo pisano del 1200, con le sue monete, i suoi commerci, i rapporti con l’imperatore Federico II, con i suoi artigiani, è passato davanti agli occhi dei miei ragazzi, attraverso la lettura di una scheda del professore Franco Ghione (I denari pisani fino alla prima metà del ‘200 ) e la spiegazione di un passo della professoressa Monica Baldassarre , riguardante le monete pisane.
Insieme agli studenti si è fatta la riflessione che le monete sono un’ importante fonte per la ricostruzione storica, ma anche un elemento in cui le tecnologie e la matematica si mettono al lavoro per costruire un prodotto estremamente raffinato da un punto di vista scientifico. Le monete antiche sono state percepite come una piccola opera d’arte dai ragazzi.

Dopo avere ragionato su problemi pratici di concentrazione molto semplici come quelli riportati nel paragrafo precedente, insieme con la classe ci siamo impegnati nella realizzazione di un modello didattico che simulasse la purificazione e determinazione del titolo dell’argento nelle monete, ispirato ad un problema di Fibonacci riportato nel capitolo VIII paragrafo II del Liber Abaci. Si tratta di calcolare la quantità di argento contenuta in una libbra di una data lega di argento e metallo povero; per fare questo si suppone che la quantità di argento P(a) contenuta in una parte a di quella lega è proporzionale ad a, in questo modo sapendo quanto argento si trova in un pezzettino di quella lega (un granulo) e sapendo il peso di quel granulo si poteva calcolare la quantità ci argento contenuta in una intera libbra senza doverla fondere.

Abbiamo analizzato dapprima le unità di misura di peso in vigore a Pisa nel 1200, comprendendo i rapporti tra di esse e cercando di spiegare l’etimologia delle parole, che sicuramente è sembrata legata ai prodotti e al commercio: i ragazzi hanno osservato come in alcuni casi le unità di peso e le unità relative al valore dei soldi si confondano le une con le altre.
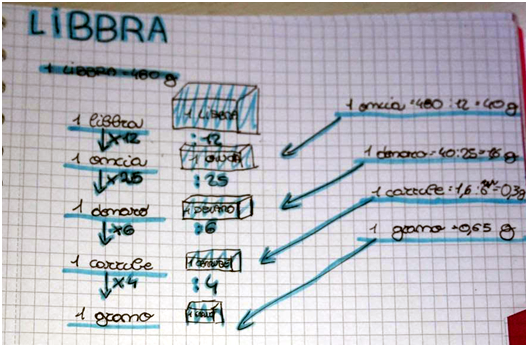
Le misure di peso al tempo di Fibonacci erano essenzialmente le seguenti:1 Libbra (circa mezzo chilo) equivalente a 12 once; 1 oncia equivalente a 25 denari di cantare; 1 denaro di cantare equivalente a 6 carrube; 1 carruba equivalente a 4 grani.
Le monete erano ricavate da una lega che conteneva una parte di argento puro e una parte di metallo povero. Da una libbra (490 gr. circa) di tale lega venivano ricavati 240 monetine dette denari; 12 denari formavano un soldo e 20 soldi una libbra.
La parola libbra (tradotta a volte con lira) viene utilizzata sia come misura di un peso, sia come una unità di conto per indicare 20 soldi. Abbiamo scoperto che cantaro [dall’arabo qinṭār] ha lo stesso etimo di quintale; che libbra in latino vuol dire «bilancia». “carruba” fa riferimento al fatto che nei mercati arabi si utilizzassero i semi di carrube per pesare le gemme preziose, grazie al loro peso e forma costanti; mentre il grano è una misura di peso, per piccole quantità, largamente usata specialmente nei paesi anglosassoni. Il nome sembra derivare dal fatto che tale unità di misura è basata sul peso medio d'un grano di frumento. Come si vede nell’immagine riportata sotto abbiamo ricostruito l’equivalenza approssimativa tra le antiche unità di misura con il sistema decimale dei grammi.

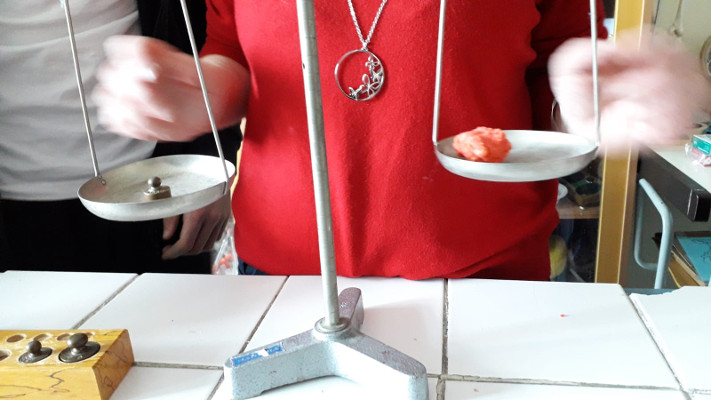
La nostra intenzione era quella di riprodurre le unità di peso con della plastilina fatta da noi, ma ci siamo resi conto che i grani erano davvero troppo difficili da realizzare e da pesare con la nostra bilancia a due bracci, rudimentale ma sicuramente molto più rappresentativa dei problemi di pesata che si potevano incontrare nel Medioevo, rispetto ad una bilancia tecnica elettronica. Così ci si sono posti problemi davvero sostanziali che si possono affrontare in un laboratorio vero: la sensibilità degli strumenti, gli errori, le approssimazioni sulle cifre decimali. Anche se la trattazione rimane quella appropriata ad una seconda secondaria di primo grado, l’occasione di riflessione è stata davvero importante e realistica.

Dopo aver compreso quali siano le caratteristiche di uno standard, ho pensato di far utilizzare i blocchi BAM per tale scopo. I ragazzi li conoscono, li abbiamo a disposizione e per i problemi con piccole unità di misura come i grani, i denari ed i carrube vanno benissimo.

  

Il pomeriggio prima dell’esercitazione in laboratorio, ho prelevato 12,5 g equivalenti a 2 di carrube di limatura di ferro colorata con glitter e li ho mescolati alla cera di una candela sciolta fino ad avere 27,2 g che equivalgono a 5 di carrube; ( naturalmente le equivalenze sono stabilite sulla bilancia tecnica con gli standard fatti con i BAM). Li ho messi a solidificare per il giorno dopo: sono il mio modello sperimentale.
Il giorno successivo propongo di pesare il campione di cera e metallo, che io chiamo come nella scheda “bolzone”. Alla pesata i ragazzi si accorgono che pesa un po’ meno di 6 carrube, quindi meno di un denaro per la precisione con un numero misto, pesa di carrube.
Propongo di analizzarlo: di dire cioè qual è il rapporto tra “l’argento” e d il “bolzone”.
Loro sanno che in passato si doveva fare coppellazione per purificare l’argento, ci chiariamo sul fatto che noi non possiamo realizzare delle reazioni chimiche ad alta temperatura e che la nostra cera è solo un esempio di minerale proveniente dalla miniera, ma che ci dobbiamo porre il problema di separare i componenti, proprio come in un metodo di purificazione qualsiasi.
L’idea è di sciogliere filtrare nelle nostre “coppelle” ( i recipienti di alluminio sono comunque delle scodelle e questa è l’etimologia). Il nostro modello ha fatto sorridere i ragazzi, a me non interessava che fosse di alto livello tecnico, piuttosto che fosse “problematico e rappresentativo”. Per l’illustrazione di quanto segue si veda la Figura 13. Nello sciogliere si sono separati i glitter, di densità minore, hanno simulato le impurezze metalliche minori. La successiva separazione è stata fatta per filtrazione: attraverso un colino la limatura di ferro, il nostro argento, è stata separata dalla cera. Il risultato è venuto dalla divisione tra  21 8 e  45 8, quindi tra 21:45 =  21 45 =  7 15, che i ragazzi hanno stimato facendo un calcolo approssimato 0,47 come un po’ meno del 50%.

Poiché, fissata una data lega di argento e rame, la quantità di argento P(a) contenuta in una parte a di quella lega è proporzionale ad a, se in 5  5 8 carrube di lega vi sono 2  5 8 carrube di argento, in 5  5 8 once di quella lega vi saranno 2  5 8 once d’argento e quindi in 12 once di quella lega cioè in una libbra vi saranno  21 × 12 45 once d’argento cioè 5 once e  3 5.

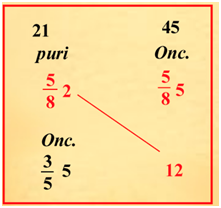
Dato che si tratta di argento cioè di un materiale prezioso, la precisione della frazione, in problemi di questo tipo è essenziale. Tornando alla nostra esperienza, se in 27,2 grammi della nostra lega vi sono 12,5 grammi di argento in un chilo di quella lega vi saranno  12,5 × 1000 27,2 = 451,2 circa grammi di argento.
Un esempio molto chiaro di come la frazione fosse un valore preciso mentre il numero decimale un valore approssimato, ma anche di come questo concetto sia molto utile nella pratica. Di qui la riflessione sul “valore” e “l’aspetto” dei numeri nelle scienze applicate e nella matematica.