
|
Parte Seconda
|
||
Parte seconda dell’ottavo capitolo sul cambio delle monete.
|
||
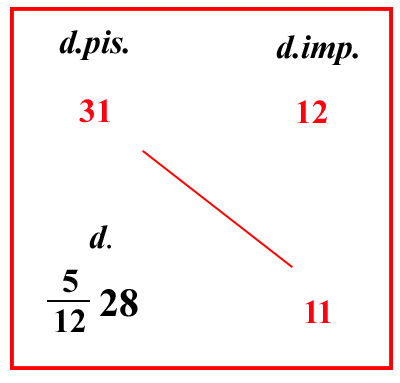
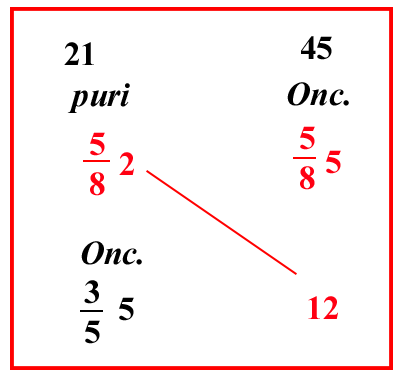
| (VIII.2.1 ; G: VIII.183) Se 1 soldo imperiale, cioè 12 denari, o qualunque altra moneta si vende per 31 denari pisanini, o per qualunque altra moneta; e si chiede quanti denari pisanini qualcuno può avere per 11 imperiali: scrivi il problema, ovviamente dapprima la vendita, cioè i 12 imperiali, poi nella stessa linea scrivi dietro il loro prezzo, cioè 31 denari pisanini; e poni gli 11 imperiali sotto i 12 imperiali, come qui si mostra: e moltiplica i numeri che sono di traverso, cioè 11 per 31, farà 341; dividili per 12, farà 51228 denari. |
|
|
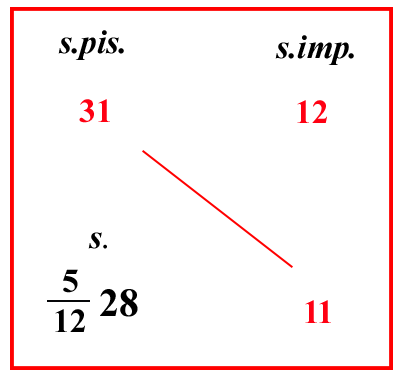
| (VIII.2.2 ; G: VIII.184) E sappi che quanti denari pisanini vale il soldo imperiale, (cioè 12 [ denari ] imperiali), altrettanti soldi pisanini valgono 12 soldi imperiali; e altrettante lire pisanine valgono 12 lire imperiali: per cui una volta detto che il soldo imperiale vale, come abbiamo detto, 31 pisanini; se si chiede quanto valgono 11 soldi imperiali, il problema si imposta così: poiché 12 soldi imperiali valgono 31 soldi pisanini, si chiede quanto valgono 11 soldi imperiali: scrivi il problema come sopra, e moltiplicherai 31 per 11, come abbiamo detto, e dividerai similmente per 12; e così farà 51228 soldi, e 5 denari pisani, come si vede nel secondo riquadro. |
|
|
Sullo stesso
|
||
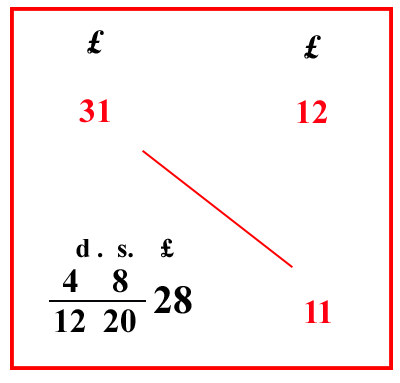
(VIII.2.3 ; G: VIII.186) Ancora se allo stesso modo vuoi sapere quanto valgono 11 lire imperiali, il problema sarà simile. Poiché 12 lire imperiali valgono 31 lire pisanine, il problema va scritto come sopra, e l’11 è da moltiplicare per il 31, e il totale è da dividere per 12, come abbiamo detto prima; e avrai 51228 lire, come si mostra in quest’altro riquadro. Poi se da 512 di una lira vorrai fare soldi, moltiplica il 5, che è sopra il 12, per 20, saranno 100 soldi; dividili per 12, che è sotto la linea di frazione, faranno 8 soldi, e 4 denari: quindi 11 lire imperiali valgono 28 lire, e 8 soldi, e 4 denari: oppure moltiplica [ per 20 ] 341 cioè il totale moltiplicazione di 31 per 11, e dividi poi per 5, e per 12, cioè per 13 di 120, e avrai soldi, e denari dalla prima divisione: perché ciò che è andato a finire sopra il 20, sono soldi; e ciò che viene sopra il 3, sono terzi di soldi, e un terzo di soldo è 4 denari. |
341×2012×20 =
341×53×20 =
18
320 28
|
|
Sullo stesso
|
||
pg.104 |
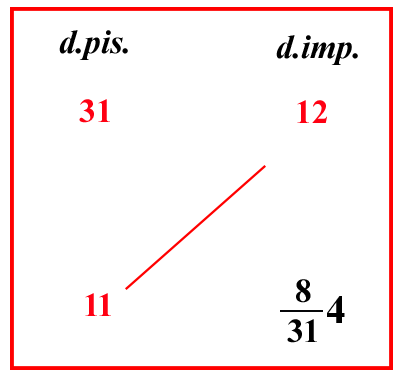
(VIII.2.4 ; G: VIII.188) Ancora il soldo imperiale vale 31 [ denari ] pisanini, come abbiamo detto; e se qualcuno chiede quanti imperiali può avere per 11 pisanini: poiché l’11 sono denari, e sono pisanini, annota i denari sopra il 31, e sopra il 12; e poni l’11 sotto il 31, cioè i pisanini sotto i pisanini, come si mostra in questo riquadro: e moltiplica 11 per 12, farà 132, dividili per 31, faranno 8314 imperiali. |
 |
Sullo stesso
|
||
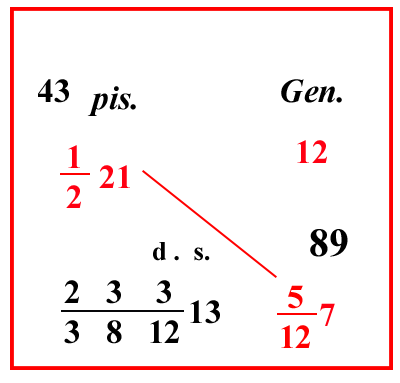
| (VIII.2.5 ; G: VIII.189) Ugualmente un soldo di Genova si vende per 1221 denari pisanini; e si chiede quanto valgono , 7 soldi e 5 denari di Genova, cioè 5127 soldi; scrivi così il problema: e moltiplica 21 per 2, e somma l’1, che è sopra il 2, farà 43, ponilo sopra 1221, e nello stesso modo moltiplica 7 per 12 e aggiungi il 5 che è sopra il 12, farà 89, ponilo sopra 5127 e moltiplica 43 per 89, farà 3827; dividilo per i soldi, cioè per 12, e per i numeri, che sono sotto la linea di frazione, cioè per 2, e per 12; questi numeri messi insieme fanno 100 3812, fanno 233 381213 soldi. |
 |
|
Sullo stesso
|
||
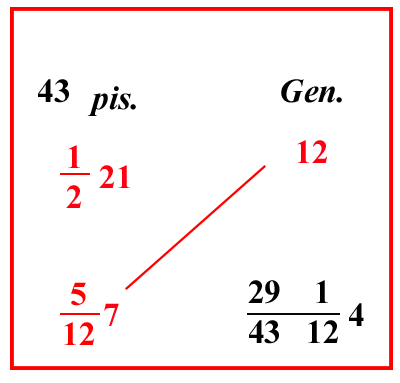
| (VIII.2.6 ; G: VIII.190) Ugualmente se al contrario, ma con lo stesso criterio, si chiede quanti genovesini avrai per 5127 soldi in moneta pisana, scrivi nel riquadro 5127 sotto 1221; poiché sono dello stesso genere, cioè dei pisani; e moltiplica 7 per 12, che sono di traverso, e dividi per 21. Questo si fa così: trova 43 e 89, e scrivi questi numeri sopra di essi, e moltiplica 89 per 12, che gli è di traverso; e per 2, che è sotto la linea dopo il 21, fa 2136; dividilo per 43, e per il 12, che sono sotto la linea di frazione dietro il 5127, fa 291 43124 soldi come si mostra in questo riquadro. |
 |
|
Sullo stesso
|
||
|
(VIII.2.7 ; G: VIII.191)
Ugualmente i soldi merguliensi
[NdT]
Secondo L.E. Sigler coniati
, cioè 12 denari, valgono in Provenza
1413 denari regali; e si chiede quanto valgono 5 lire, e 13 soldi, cioè
13205 merguliensi: quando chiede il cambio in lire, tale è la richiesta, visto che 12 lire merguliensi valgono
1413 lire regali: scrivi così il problema; e arriva a
1413, moltiplicando 13 per 4, e aggiungendo 1, fa 53: poi moltiplica 5 per la sua linea di frazione, fa 113; e moltiplica 53 per 113, fa 5989; dividilo per 12, e per 4, e per 20, che sono sotto la linea , fa lire
194
412206. Invece se hai 5 lire, e 13 soldi regali, e vuoi ottenere da questi merguliensi, scrivi allora
13205, sotto
1413, perché sono dello stesso genere; e moltiplica
13205 per 12, che sono di traverso, e dividi per
1413, cioè moltiplica 113 per 12; e per 4, che è dopo il 13, fa 5424: dividilo per 53 e per il 20 della linea di frazione, ma prima moltiplica 5424 per 12, per averlo nella linea di frazione dopo il 20, fa
442
5312205 merguliensi.
a Maguelon in Provenza |
||
|
(VIII.2.8 ; G: VIII.193)
Ugualmente soldi barcellonensi
[NdT]
Coniati a Barcellona
, cioè 12 denari, valgono
2317 podiensi
[NdT]
Secondo L.E.Sigler coniati a Padova
; e qualcuno chiede quanti podiensi avrà per 31 lire, e 14 soldi, e 9 denari barcellonensi, scrivi il problema come qui si mostra; e moltiplica
2317 per
914
122031, che sono di traverso, e dividi per 12, fa
15514
26122046 podiensi.
|
||
Sullo stesso
|
||
pg.105 |
(VIII.2.9 ; G: VIII.194) In verità se preferisci che queste 914 122031 lire siano podiensi, e vuoi ottenere da esse i barcellonensi, scrivi dunque i podiensi sotto ai podiensi, come è mostrato in questo problema; e moltiplica 12 per 914 122031, e dividi per 2317, cioè moltiplica il detto 12 per 7617, che sono di traverso; e per 3, che è sotto la linea di frazione dopo il 17, e dividi per 53, e per 10 1220, che sono sotto la linea di frazione dopo il 31, farà 43111 53122021 lire. | |
|
(VIII.2.10 ; G: VIII.195)
Ad oggi soldo imperiale vale
1428 [ denari ] pisanini, e in più ciascuna lira imperiale vale
121 denari; e si chiede quanti pisanini si possono avere per 21 lire e
145 denari imperiali, cioè per
150
4122021 lire: poiché il soldo è un ventesimo di lira, dividi
121 per 20, fa
11
220 di un denaro pisanino; sommalo col valore dei soldi, e così 12 [ denari ] imperiali valgono
16
22028 pisanini, e 12 lire imperiali ne valgono
16
22028; poni così
150
4122021 sotto le 12 lire imperiali, e le moltiplicale per
16
22028; e dividi il totale per 12, e avrai quanto proposto. E se il soldo imperiale vale
1428 pisanini, e meno
121 denari ciascuna lira imperiale, dividi di nuovo
121 denari per 20, fa
11
220; sottraili da
1428, restano
13
22028 come prezzo di un soldo imperiale.
Per cui se hai
150
4122021
[NdT]
31 è un chiaro errore
lire pisanine, dalle quali vuoi degli imperiali, moltiplicale per 12, e dividi per
13
22028. E annota quanti denari sono dati per la lira, più o meno del valore del soldo; aggiungi o sottrai dallo stesso valore tutti i ventesimi, e avrai il valore dello stesso soldo.
|
1 soldo imperiale vale:
28 + 1 4 + 11 220 denari pisanini  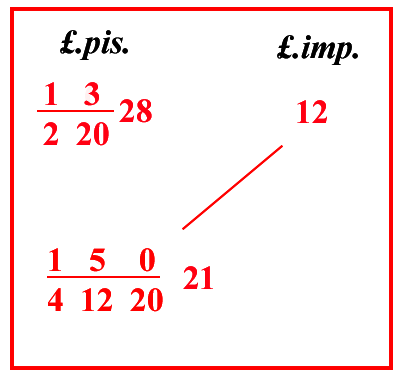 |
|
Commento sul cambio delle monete che sono vendute in soldi.
Inizio del cambio delle stesse quando si vendono in lire di denari |
||
|
(VIII.2.11 ; G: VIII.197)
Una lira in pisanini, cioè 20 soldi, vale 1 lira in bolognini
[NdT]
Moneta in uso a Bologna dal 1191
, e in più 54 bolognini, cioè 20 soldi in pisanini valgono
1224 in soldi bolognini. Perciò 20 pisanini valgono
1224 bolognini; e 20 lire in pisanini, valgono
1224 [ lire in bolognini ] ; si chiede quanti bolognini si hanno per
1411 pisanini: scrivi il problema come qui si mostra; e moltiplica
1411 per
1224, e dividi per 20 pisanini, fa
16
4813 bolognini: e se il cambio delle lire pisane è
1256 bolognini, cioè se 20 soldi pisanini valgano 24 soldi, e
128 denari, cioè
18
21224, e vuoi sapere quanti pisanini valgono 14 soldi, e 5 denari bolognini, poni
51214 soldi sotto
18
21224 soldi, e moltiplica
51214 per 20, e dividi
18
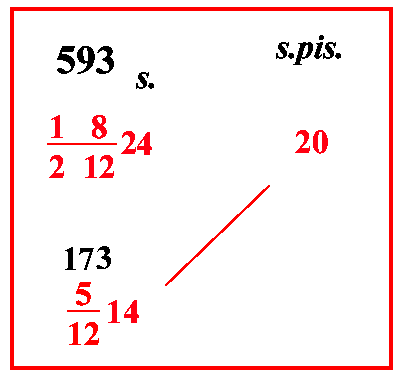
21224, cioè moltiplica 173 per 20; e per 12, e per 2, che sono sotto la linea di frazione; e dividi per 593, e per 12, che sono sotto la linea di frazione di 14, avrai soldi [ 208
5931211 ]
|
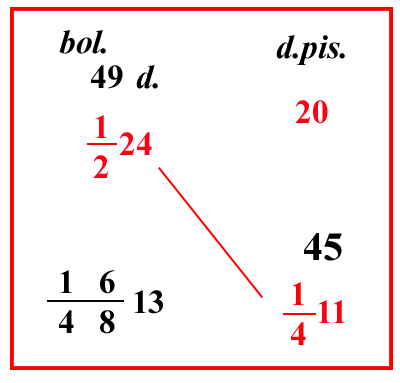
54 denari sono 4 soldi e 6 denari cioè 4 soldi e mezzo.
  |
|
| (VIII.2.12 ; G: VIII.198) Ancora il cambio della lira pisanina è 3457 bolognini, cioè 20 soldi pisanini valgono 39 41224; e si chiede quanti bolognini valgono 17 lire, e 11 soldi, e 5 denari pisanini; scritto il problema moltiplica 511 122017 per 39 41224 lire, e dividi per 20 lire pisanine, hai [ 12141115 2820122021 ] il risultato in bolognini. E se hai 511 122017 lire in bolognini, moltiplicale per 20, e dividi per 39 41224, e avrai quanto proposto. | ||
|
(VIII.2.13 ; G: VIII.200)
Dunque il soldo imperiale vale
1228 pisanini; si chiede quanti bolognini si hanno in cambio di una lira pisanina: poiché il soldo imperiale vale 36 bolognini, allora
1228 pisanini valgono 36 soldi bolognini; e
1228 lire pisanine valgono 36 lire bolognine. Perciò
1228 lire pisanine hanno un cambio di
127 bolognine, ( da
1228 a 36) : e poiché chiedi il cambio di una lira, poni 1 sotto
1228 libre, come si vede in questo riquadro; e moltiplica 1 per
127 e dividi per
1228, cioè moltiplica 1 per 15, e dividi per 57: ma perché tu abbia nella frazione
10
1220, moltiplica la detta moltiplicazione di 1 in 15 per 80; sarà 1200; dividilo per
100
191220, farà
335
191220 denari: cioè
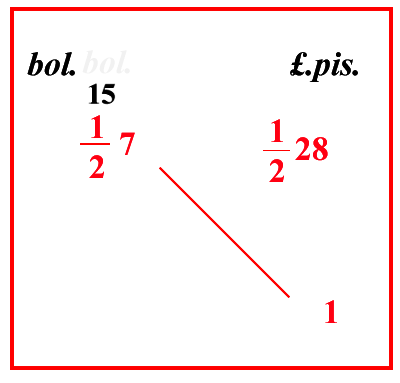
31963 denari, e tanto è il cambio delle lire pisane. E se al contrario si dice: il cambio di una lira pisana è [ 1 lira e ] 5 soldi, e 3193 denari [ bolognini ], cioè 20 soldi pisanini valgono 33 191225 soldi bolognini; e si chiede quanti pisanini valga il soldo imperiale, per quello stesso soldo poni 3 soldi sotto 33 191225; perché il soldo imperiale vale 3 soldi di bolognini; e moltiplica questo 3 per il 20 che gli è di traverso, e dividi per 33 191225; cioè per 51925, dato che 33 1912 sono solo 519, fa 14 2122, cioè 1228 denari come valore di un soldo imperiale. |
Chiede cosa si ha in più cambiando 1 lira pisana in lire bolognine passando dai soldi imperiali.
  |
|
pg.106 |
(VIII.2.14 ; G: VIII.203) Ancora un soldo imperiale vale 3428 pisanini meno 142 denari per qualunque lira imperiale; e si chiede quanti bolognini si hanno in cambio per 1 lira di pisanini; per i detti 142 denari, sottrai 12 420 da 3428 pisanini, cioè da 152028 pisanini, rimangono 312 42028 come valore di un soldo imperiale. Quindi lire 312 42028 in pisanini, cioè 28 lire, e 12 soldi, e 9 denari di pisanini valgono 36 lire in bolognini. Perciò il cambio di 28 lire, e 12 soldi, e 9 denari, è 7 lire, e 7 soldi, e 3 denari in bolognini, che sono da 28 lire, e 12 soldi, e 9 denari fino a 36 lire. Perciò scrivi il problema come qui si mostra; e moltiplica 1 per 17 4207, e dividerai per 312 42028; farà 160915 22911220. |
Valore del soldo imperiale:
3 428 - 12 420 = 312 42028 denari 36 - 312 42028 = 17 4207 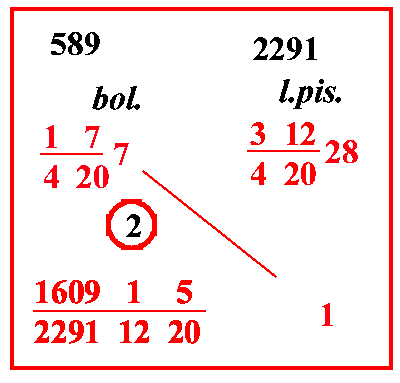 |
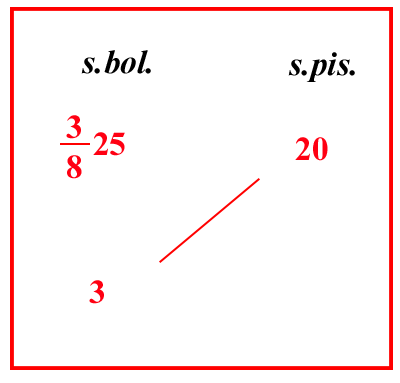
| (VIII.2.15 ; G: VIII.205) Ancora, il cambio di lire pisane è di 1264 bolognini, cioè 3825 soldi in bolognini valgono 20 soldi in pisanini e si chiede il prezzo di 3 soldi in bolognini, cioè di 1 soldo in imperiali : scritto così il problema, moltiplica 25 per la sua frazione, fa 203: moltiplica quindi 3 per 20; e per 8, fa 480, che vanno divisi per 203, cioè per 10 729: ma moltiplicalo per 20 e per 12, fa 155200 ; dividilo per 1000 7292012, fa 11474 72920122, cioè 1147 7292028 denari. E annota che ho messo 120 dopo [ cioè a sinistra di ] 112 perché cada sopra quei ventesimi di denari, che toccano al soldo ; perché quanti ventesimi toccano al soldo, tanti denari toccano a una lira : quindi il soldo imperiali vale 28 denari pisanini, e in più 114 7297 denari per ciascuna lira imperiale. Ma dai cinque denari che riguardano la lira tocca al soldo la quarta parte di un denaro , e per 10 denari se ne ha 12; e per 15 denari toccano al soldo 34 di un denaro. Dunque il soldo in imperiali vale 1428, e più di 114 7292 denari per lira, cioè poco meno di 122 denari. Per cui il soldo imperiale vale 1228 meno 122 denari per ciascuna lira ; e impegnati a fare così per le cose simili. |
 |
|
Dei veneziani, quando si vendono quantità con riferimento al peso e si cerca il prezzo del peso della lira
|
||
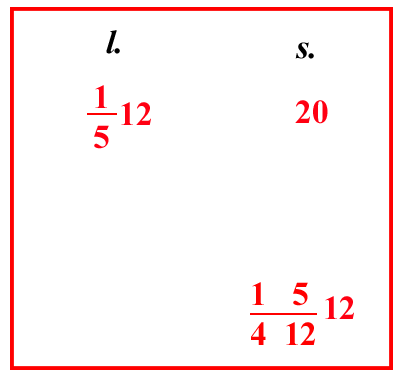
| (VIII.2.16 ; G: VIII.208) La lira veneziana, cioè 20 soldi, si vende per 12 lire, e 4 soldi in pisanini ; si chieda quanto vale la lira con riferimento al peso degli stessi, che poniamo essere di 12 soldi e di 145 denari : moltiplica 15 41212 per 1512, e dividi per 20; invece la lira rispetto al peso dei veneziani vale 128 lire; e vuoi sapere il valore delle lire rispetto ai valori numerici, cioè dei 20 soldi, moltiplica 20 per 128, e dividi per 15 41212, e così avrai senza dubbio quanto proposto. |
 |
|
Della libbra d’argento
|
||
| pg.107 |
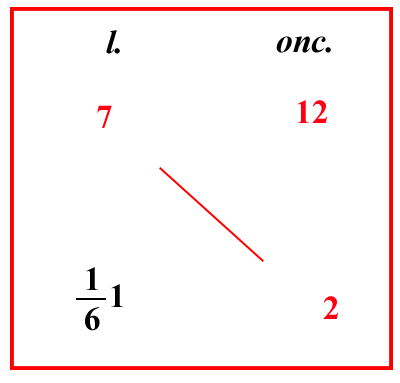
(VIII.2.17 ; G: VIII.209)
Se una libbra d’argento, cioè 12 once è venduta per 7 lire ; e si chiede quanto valgono 2 once, scrivi nel riquadro once sotto once, cioè 2 sotto il 12, e moltiplica il 2 per il 7, che sono di traverso, farà 14 ; e dividi per 12, fa
161 lire in denari, cioè 23 soldi e 4 denari, come si vede in questo riquadro. O altrimenti : poiché 2 once sono
16 di una libbra, prendi
16 di 7 lire, che è corrispondente a 23 soldi, e 4 denari, come abbiamo detto prima. Ugualmente se la libbra d’argento si vende per 7 lire, e 9 soldi, cioè 9207 lire, e si chiede quanto valgono 142 once, scrivi il problema, come qui si mostra, e moltiplica 142 per 9207, e dividi per 12, fa 1117 412201 lire. Ugualmente se la libbra vale 7 lire, e 11 soldi [ e 5 denari ], cioè 511 12207 ; e si chiede quanto valgano 7 once e 14 denari di cantaro, cioè 14257 once: poiché le once pesano 25 denari di cantaro ; scrivi il problema come qui si mostra, e moltiplicherai 511 12207 per 14257 e dividerai per 12 : fa 017415 3101012204 lire. |
 |
Sullo stesso
|
||
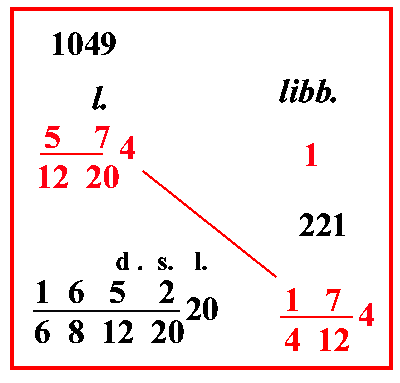
| (VIII.2.18 ; G: VIII.212) Ugualmente la libbra d’argento si vende per 57 12204 in [ lire ] regali ; e si chiede quanto valgano 4 libbre e 147 once, cioè 17 4124 libbre. Poiché si cerca il prezzo delle libbre in questa posizione, si deve scrivere solo 1 per la vendita, cioè per la libbra, affinché ambedue siano fatte di una sola qualità così come sono dello stesso genere, come qui si mostra ; moltiplica 17 4124 per 57 12204, e dividi per 1, cioè per le libbre, fa 1652 68122020 lire in regali. |
 |
|
Sullo stesso
|
||
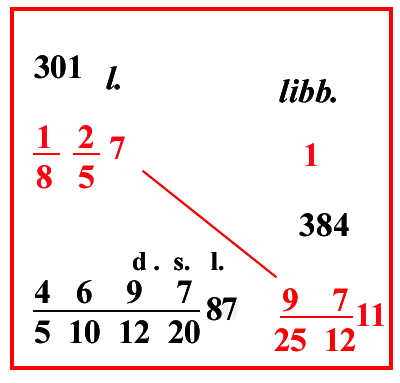
| (VIII.2.19 ; G: VIII.213) Ugualmente se la libbra d’argento si vende per 18257 lire ; e si chieda quanto valgano 11 libbre, e 7 once, e 9 denari di cantaro, cioè 97 251211 libbre : moltiplica i numeri, che sono di traverso, cioè 18257 per 97 251211, e dividi per la vendita, cioè per 1, fa 4697 510122087 lire. |
 |
|
|
(VIII.2.20 ; G: VIII.214)
Ugualmente
19147 lire libbre d’argento per
182563 lire bizanti saraceni ; e si chiede quanto valgano 5 once, e 11 denari di cantaro, e 5 carrube
[NdT]
25 denari di cantaro fanno 1 oncia,
, cioè
511
6255 once : poiché
19147 libbre e
511
6255 once sono di una stesso genere, cioè di argento, ma non sono di un’unica qualità ; perché
19147 sono libbre e
511
6255 sono once, o dalle
19147 libbre si fanno once o dalle
511
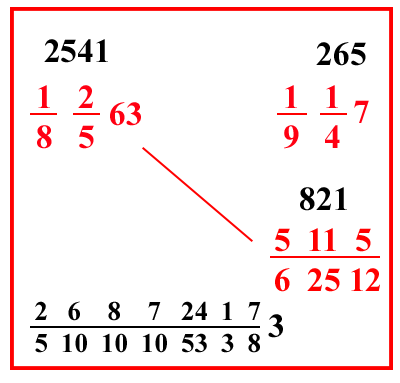
6255 once si fanno parti di una libbra ; e scrivi il problema come qui si mostra, e moltiplica 7 per le sue frazioni, fa 265. Ugualmente moltiplica 63 per le sue frazioni, il risultato è 2541 ; e moltiplica il 5 che è sopra il 12, per la sua frazione, fa 821, moltiplicalo per 2541, e per 4, e per 9, che sono sotto le frazioni sotto 265 e dividi per la regola del 265 e per tutti gli altri fratti, ordinando perché tu abbia
10
38 nella frazione della divisione per carati, farà
26872417
510101053383 bizanti saraceni
[NdT]
6 carube fanno 1 denaro di cantaro
I bizanti saraceni
.
sono suddivisi in 24 carati |
 |
|
Sullo stesso
|
||
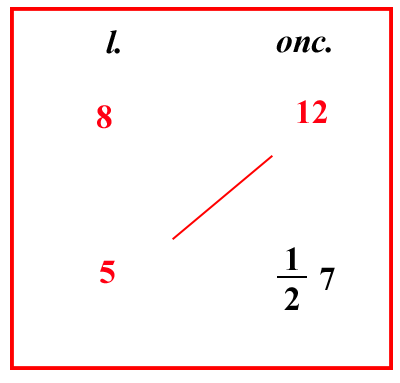
| (VIII.2.21 ; G: VIII.216) Ancora se si stabilisce che la libbra di argento , cioè 12 once, vale 8 lire ; e qualcuno vuole sapere quanto argento avrà per 5 lire di denari ; scrivi 5 sotto 8 nel riquadro, e moltiplica 5 per 12, farà 60 ; dividilo per 8, farà 127 once , come si mostra nel riquadro. |
 |
|
Sullo stesso
|
||
| (VIII.2.22 ; G: VIII.217) Ancora la libbra di argento vale 7 lire ; e qualcuno vuole sapere quanto argento avrà per 4 lire. Scritto pertanto il problema, moltiplica 4 per 12, fa 48 ; e dividilo per 7, fa 676 once. In verità se da 67 di un’oncia, vuoi sapere quanti denari di cantaro valgono, poiché l’oncia pesa 25 denari [ di cantaro ], moltiplica il 6, che è sopra il 7, per 25, fa 150 ; e dividi per 7, fa 3721 denari di cantaro. Ancora se da di un denaro vorrai fare carrube, moltiplica il 3, che è sopra il 7, per 6 ; e poiché un denaro è 6 carrube, fa 18 ; e dividi per 7, fa 472 carrube ; quindi per quelle 4 lire avrai 6 once, e 21 denari [ di cantaro ], e 472 carrube. Poi se vorrai avere lo stesso risultato con un accorgimento migliore, in una sola moltiplicazione e divisione, moltiplica il 48 scritto sopra per le parti di un’oncia, cioè per il numero dei denari, e delle carrube, , cioè per 25 e per 6, fa 7200 ; dividilo per 100 7625, cioè per 1000 7655, che è più facile, e avrai la stessa quantità, come è descritto sopra nel riquadro : e nello specifico ciò che verrà sopra il 7, sono parti di una carruba; e ciò che viene sopra il 6 sono carrube ; e quello che è sopra 10 55 sono denari di cantaro ; e quelle fuori dalla frazione sono once così come lo sono quelle 12 vendute sotto le quali sono scritte, perché sempre quale è in genere e in qualità il numero sotto il quale si scrive il risultato, tale sarà anche quello che si trascrive sotto di esso. | 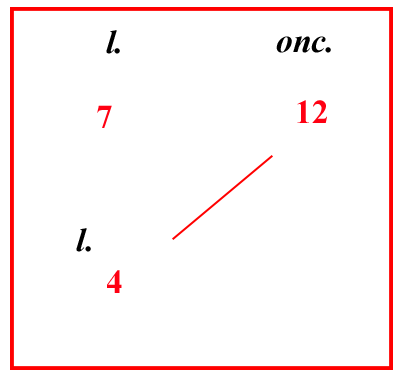 |
|
pg.108 |
(VIII.2.23 ; G: VIII.220) Perciò [ partendo ] dallo stesso numero sotto il quale si deve porre il totale, cioè il quarto numero ignoto che comprende tutto ciò che devi avere in cima alla linea della divisione; se quello che è scritto sopra il posto vuoto sono lire e denari fa in modo di avere 10 1220 per soldi e denari : e se sono soldi, fa in modo da avere 1 12 per i denari. e se sono tareni, fa in modo di avere 1 12 per i grani. E se sono bizanti saraceni, o yperperi, fa in modo di avere 10 38; e se fossero bizanti di Garbo, fa in modo di avere 1 10; e se sono state libbre, o rotoli di qualche merce non molto cara, come il pepe, fa in modo di avere 1 12 per le once ; e se fossero state libbre pisane di qualche merce più cara come lo zafferano, fa in modo di avere 100 5512 per le once e i denari di cantaro; e se sono libbre dello stesso peso di cose ancora più care, come l’argento, fa in modo di avere 1000 65512 per le once i denari e le carrube : e se sono libbre di una cosa più cara, come l’oro, fa in modo di avere 10000 465512 per le once, i denari, le carrube e i grani ; e se sono once d’oro di libbre pisane, fa in modo di avere 1000 4655 per i denari di cantaro, e le carrube, e i grani : e se sono denari di cantaro d’oro , fa in modo di avere solo 10 46 per le carrube e grani : e se sono carrube d’oro , o qualcosa di più caro, fa in modo di avere solo 1 4 in linea di frazione per i grani, e se sono once d’argento , basta che tu abbia solo 100 655 per i denari e le carrube, come scriviamo ordinatamente nel riquadro sopra. e se sono denari di cantaro di argento , è sufficiente che tu abbia solo 1 6 per le carrube ; e se sono marche di argento , fa in modo di avere 1000 6558 per le once e i denari e le carrube ; e così deve essere fatto in tutte le altre situazioni secondo la diversità dei pesi e delle loro parti e secondo la consuetudine e il sistema di quelle province, nelle quali dovrai operare. Pertanto se terrai in buon conto, ciò che è stato detto, avrai con una sola moltiplicazione, e con una sola divisione quello che ti serve per le cose richieste : e per non dimenticarti di salvare ciò che talora hai nella divisione dalla parte o dalle parti dei numeri prescritti, che devi porre in cima alle linee di frazione [ cioè a destra ], e unirla, o unirle con quelli, che ti mancano da quei numeri, e moltiplicare con gli stessi. Per esempio : poniamo che ti occorra avere 1 12 in cima alla linea di frazione per i denari o le once, e hai da ciò 1 4 nella divisione ; si toglie quindi a te 1 3, uniscili insieme facendo da loro 1 12, che metti in cima alla linea di frazione ; e moltiplica tutto il totale per 3, per quel 1 3 che si è stato tolto prima. Infatti se dalla divisione, nella quale devi dividere tutto ciò, potrai prendere ciò che ti è necessario avere in cima alla linea frazione, fa in modo di prenderlo; e ponilo in cima alla linea di frazione. Per esempio: ci occorre avere 10 1220 per soldi e denari; e dobbiamo dividere il totale per 10000 268910 uniamo quindi 1 2 con 1 10 e facciamo da loro 1 20, poi uniamo 1 6 con 1 8 e facciamo da loro 10 412, e così abbiamo in linea di frazione 1000 491220, che è tanto quanto 10000 268910. |
Misure monetarie
 Misure di peso
 |
| (VIII.2.24 ; G: VIII.227) Ancora, se nella divisione non hai nulla di ciò che ti è necessario avere in cima alla linea di frazione, moltiplica tutto il totale per ciò che ti è necessario avere in cima alla linea di frazione, e in più aggiungi alla divisione ciò che devi avere in cima alla linea di frazione. Per esempio : poniamo che si debba dividere 321 per 10 711 e ci occorre avere 10 38 in cima alla linea di frazione per i carati ; moltiplica 321 per 3, e per 8, cioè per 24 ; e questo è fare carati da 321 bizanti, e dividi per 1000 71138; e così si intenda del resto : e noi in seguito spiegheremo singolarmente ogni singola cosa. | ||
Sul marco
[NdT]
Unità di misura ponderale introdotta a Colonia e diffuso a partire dal XII secolo nell’Italia centro settentrionale.
d'argento.
Diviso in 8 once del peso di 2/3 circa della libbra. |
||
pg.109 |
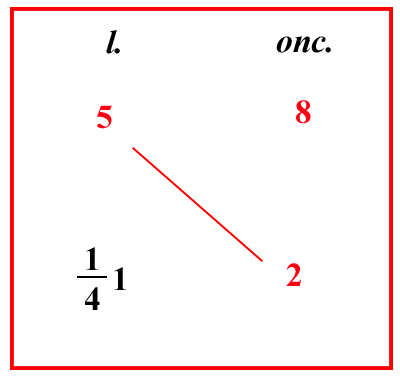
(VIII.2.25 ; G: VIII.228) Se un marco d'argento, cioè 8 once, si vende per 5 lire; e si chieda quanto valgono 2 once: scrivi nel riquadro once sotto once, cioè il 2 sotto l'8 come qui si mostra, e moltiplica il 2 per il 5 che sono di traverso, fa 10; dividilo per 8, fa 1 41 lira, cioè 25 soldi, come si mostra nel riquadro. O, altrimenti, poiché le 2 once sono la quarta parte di un marco, cioè di 8 once, prendi 1 4 del prezzo del marco, cioè delle 5 lire, faranno 25 soldi, come abbiamo detto precedentemente. |
 |
Sullo stesso
|
||
|
(VIII.2.26 ; G: VIII.229)
E se con lo stesso sistema chiedi quanto argento devi avere per 2 lire, scrivi prezzo sotto prezzo, cioè il 2 sotto il 5, e moltiplica il 2 per l'8, fa 16; e dividerai per 5, farà
1
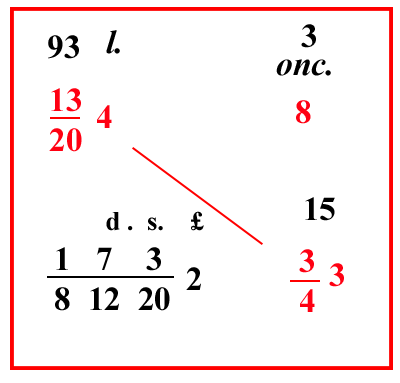
53 once, cioè 3 once e 5 denari di cantaro, poiché l'oncia del marco e della libbra è la stessa. Ugualmente un marco si vende per 4 lire e 13 soldi, cioè per 13 204 lire; quanto valgono 3 43 once: scrivi il problema, come qui si mostra, e moltiplica il 3 43 per 13 204, e dividi per 8, cioè moltiplica 15 per 93, che fa 1395, e dividi per 100 4820: ma per avere il 12 dopo il 20 nella frazione, unisci 1 4, che è nella divisione, con 1 3 e otterrai il 12; e moltiplica 1395 per 3, e dividi il totale per 100 81220, e poni il 3 sopra l'8 in modo da tenerlo meglio a mente per la prova, farà 173 812202 lire. |
 |
|
Sullo stesso.
|
||
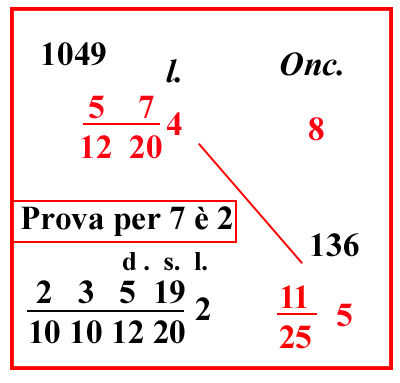
| (VIII.2.27 ; G: VIII.231) Ugualmente un marco d'argento si vende per 57 12204 lire; e si chiede quanto valgono 5 once e 11 denari di cantaro, cioè 11 255 once. Scrivi il problema così, e moltiplica il 4 per la sua frazione; risultano 1049 denari, ponili sopra, e moltiplica 5 once per 25 e aggiungi 11, fanno 136 denari di cantaro; poi moltiplica 136 per 1049, e dividerai per 8 e per tutti i fratti e metterai 10 1220 all'inizio della frazione: poiché il numero che è sopra il posto vuoto nel quale dobbiamo porre il risultato è il numero delle lire, fa 23519 101012202 lire. |
 |
|
Sullo stesso.
|
||
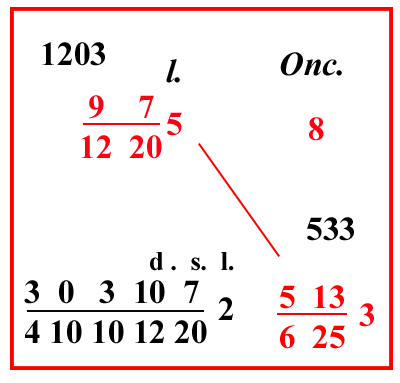
| (VIII.2.28 ; G: VIII.232) Se un marco di argento si vende per 5 lire, e 7 soldi, e 9 denari, cioè 97 12205 lire, e si chiede quanto valgono 3 once e 13 denari di cantaro e 5 carrube, cioè 513 6253, scrivi il problema come qui si vede, e moltiplica 513 6253 per 97 12205, e dividi per 8, fa 303107 4101012202 lire. |
 |
|
Sullo stesso.
|
||
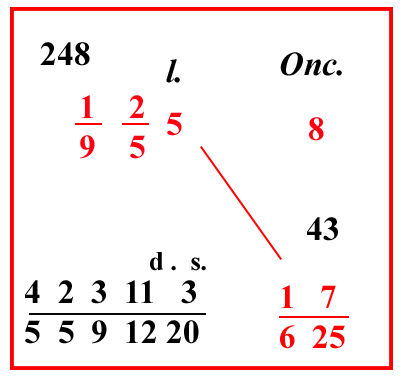
| (VIII.2.29 ; G: VIII.233) Ugualmente se un marco si vende per 1 92 55 lire; e si chiede quanto valgono 7 denari di cantaro, e 1 carruba, cioè 17 625 di un'oncia, scrivi così il problema; e moltiplica 17 625 per 1 92 55 e dividi per 8, fa 423113 5591220 di una lira. |
 |
|
pg.110 |
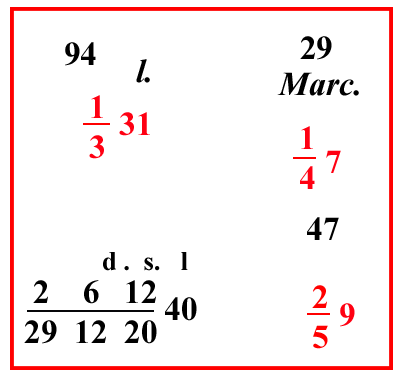
(VIII.2.30 ; G: VIII.234) Ugualmente se 1 47 marco si vende per 1 331 lire; quanto valgono quindi 2 59 marchi: scrivi così il problema; e moltiplica 7 per 4, e somma l'1, fa 29; e moltiplica 31 per 3, e somma l'1, far 94; e 9 per il 5 e somma 2, fa 47; e moltiplica 47 per il 94; e per il 4 che è sotto il 29, fa 17672; e dividi per 29 e per gli altri fratti, cioè per 3, e per 5, che sono sotto la linea di frazione: ma poiché sappiamo che il totale che ne uscirà sarà il totale delle lire; e poiché il luogo nel quale le dobbiamo scrivere è sotto le lire, cioè sotto 1 331, per questo è necessario che noi si abbia all'inizio della frazione 10 1220 per avere i soldi e i denari dopo le lire. Ma poiché di 1 12 non abbiamo altro se non 1 3, sappiamo che ci manca di esso 1 4; e poiché di 1 20 non abbiamo altro che 1 5, sappiamo che ci manca per esso un altro 1 4. Dunque ci manca 16 tra entrambi; ponilo sopra il 29, e moltiplica 17672 per 16 e dividi il totale per 100 291220, si ottengono 2612 29122040 lire. |
 |
Sullo stesso.
|
||
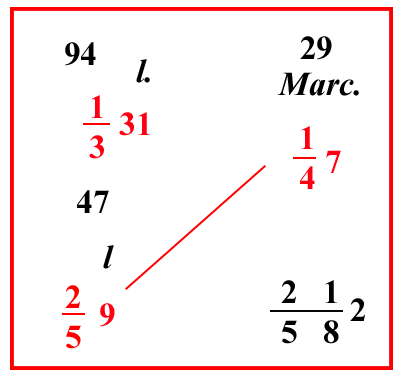
| (VIII.2.31 ; G: VIII.237) Invero, se con lo stesso sistema chiedi quanto argento uno avrà per 2 59 lire, scrivi il problema così, e moltiplica il 47 per il 29, e per 3, e dividi per la regola del 94; cioè per 10 247, e per gli altri fratti, vale a dire per 4 e per 5. Solo ometti di moltiplicare 47 e di dividere per 47: quindi moltiplica solo il 29 per il 3, che sta sotto la linea di frazione davanti al 31, fa 87; dividilo per 10 45 e per 1 2 che resta dalla regola di 94, cioè per 10 58. Ma sappiamo che ciò che risulterà dalla divisione sarà il totale di marchi, e che il luogo in cui lo dobbiamo porre è sotto i marchi, vale a dire sotto 1 47; per cui bisogna che noi abbiamo in cima alla frazione 1000 6558 per le once, i denari e le carrube: di questi abbiamo nella divisione 10 58, dunque ci manca 10 65, cioè 30. Per questo 30 dobbiamo moltiplicare l'87 in modo da ottenere 1000 6558 nella divisione. Ma poiché nella divisione scritta precedentemente i fratti sono solo parti di marco, vale a dire 10 58, non serve altro che dividere l'87 per 10 58, farà 21 582 marchi, cioè 2 marchi e un'oncia e 10 denari di cantaro. |
 |
|
Dell’oncia d’oro pisana.
|
||
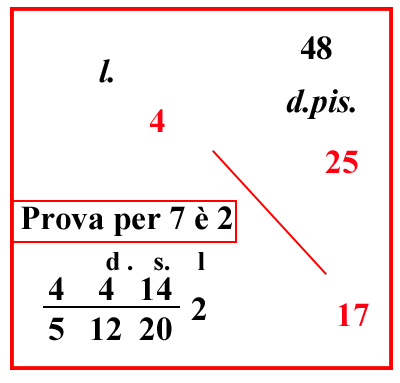
| (VIII.2.32 ; G: VIII.240) Posto che un'oncia pisana d'oro o di tareni, che pesa 25 denari di cantaro si venda per 4 lire e si chiede quanto valgono 17 denari di cantare dello stesso oro: scrivi nel riquadro 17 sotto il 25 ; poiché sono dello stesso genere, cioè d'oro, e dello stesso peso, cioè dei denari; e moltiplica le 4 lire per 17; poiché sono di traverso, fa 68 libre: moltiplica 68 per il 48 che ci manca da 10 1220; perché di essi non abbiamo altro che 1 5 e dividi il totale per 100 51220, fa 4414 512202 lire, come si mostra in questo riquadro. |
 |
|
Sullo stesso.
|
||
|
(VIII.2.33 ; G: VIII.241)
Ugualmente se la stessa oncia si vende per
3
204 lire e si chiede quanto valgono 9 denari [ di cantaro ] e 5 carrube, cioè
5
69 denari. Scrivi il problema, e moltiplica 4 per 9 e dividerai per 25, cioè moltiplica 83 per 59, farà 4897 che dividerai per il 25 e per i fratti, cioè per 6 e per 20. Ma affinché tu abbia
10
1220 nella linea di frazione, moltiplica 4897 per il 2 che ci manca da
1
12, poiché abbiamo in tale divisione, fa 9794 che devi dividere per
1000
551220, fa
43712
5512201 lira, cioè 32 soldi e
43
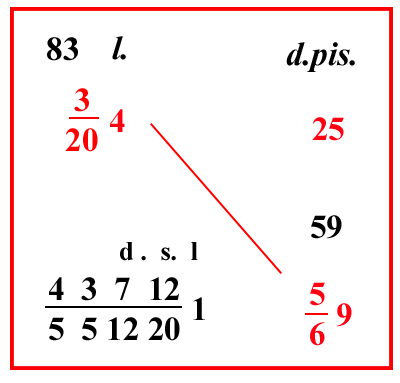
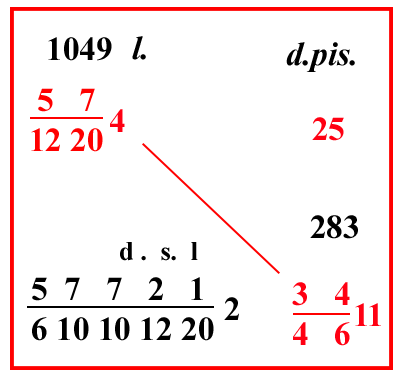
557 denari, come si mostra nel riquadro. Ugualmente se la stessa oncia si vende per 57 12204 lire; quanto valgono allora 11 denari [ di cantaro ] e 4 carrube e 3 grani, cioè 34 4611 denari: scrivi il problema come qui si mostra, e moltiplica 57 12204 per 34 4611, e dividi per 25, fa 57721 6101012202 lire come si mostra nel riquadro. |
  |
|
Sullo stesso.
|
||
pg.111 |
(VIII.2.34 ; G: VIII.243)
Ugualmente se la stessa oncia si vende per
1
34 lire e si chiede quanto valgono 13 once, e 14 denari [di cantaro], e 5 carrube, e 3 grani, cioè
3514
462513 once. Poiché si chiede in questo problema il prezzo delle once, dobbiamo scrivere 1 per l'oncia in vendita, come qui si mostra; e poi moltiplica
1
34 per
3514
462513 e dividi per 1, fa
11618
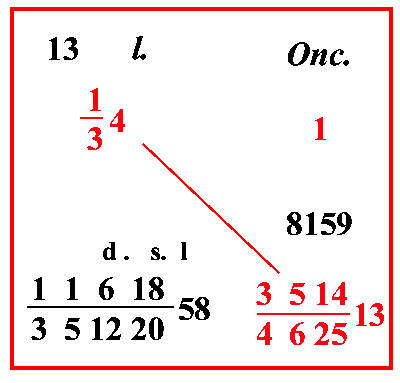
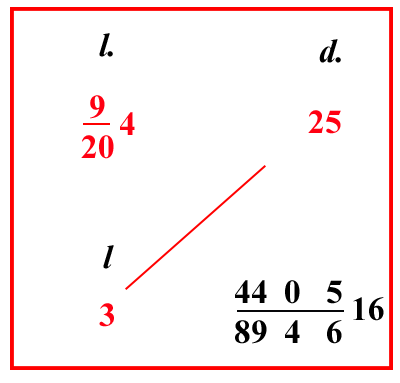
35122058 lire. Ugualmente se un'oncia si vende per 9 204 lire, e si chiede quanto qualcuno avrà della stessa oncia per 3 lire: scrivi il problema così, e moltiplica il 3 per il 25, fa 75; che devi dividere per 9 204, cioè moltiplica 75 per il 20 della frazione, fanno 1500; e dividi per 89, farà 76 8916 denari di cantaro; di questi 76 89, se vorrai farne carrube, moltiplica 76 per il numero di carrube di un denaro, cioè per 6, fa 456; dividilo per 89, ne vengono 11 895 carrube. Invero, se vuoi fare la stessa cosa con un sistema migliore, moltiplica 1500 per il 6 delle carrube; e per il 4 dei grani, farà 36000; dividilo per 100 8946, faranno 4405 894616 denari di cantaro, come si mostra nel riquadro. |
  |
Sullo stesso
|
||
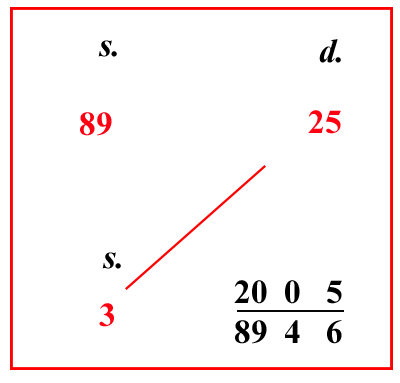
| (VIII.2.35 ; G: VIII.245) Invero se con lo stesso sistema vuoi sapere quanto avrai per 3 soldi, fai in soldi le 9 204 lire, sono 89 soldi; sotto i quali poni i 3 soldi nel riquadro; e moltiplica 3 per il 25, fa 75; moltiplicalo per 24 per avere le carrube, e i grani nella linea di frazione; e dividi il totale per 100 8946, fa 2005 8946, cioè 5 carrube e 20 89 di un grano, come si mostra nel riquadro. |
 |
|
|
(VIII.2.36 ; G: VIII.246)
Una persona volle comprare argento misto con stagno, volgarmente chiamato falso argento. Poiché non sapeva quanto argento puro ci fosse nelle libbre di quella lega d'argento, prese di esso un granulo, il cui peso era 5 carrube e
1
22 grani, cioè
5
85 carrube; e lo pose sopra il fuoco, per ripulire l'argento dallo stagno: fatto ciò, vi trovò ì 2 carrube e
1
22 grani, cioè
5
82 carrube di argento puro; si chiede quanto argento puro c’era nelle libbre di quella lega d'argento. Innanzitutto bisogna notare che poiché le
5
85 carrube sono dello stesso peso delle
5
82; come nelle
5
85 carrube di quella lega d'argento ci sono
5
82 carrube di puro argento, così in
5
85 denari [ di cantaro ] di lega d'argento ci saranno
5
82 denari [ di cantaro ] di puro argento. E in
5
85 once di lega, ci saranno
5
82 once di puro argento, similmente anche in
5
85 libbre di lega ci saranno
5
82 libbre di puro argento. Perciò, poiché in questo problema si chiede delle libbre, cioè delle 12 once, scrivi nel riquadro che nelle
5
85 once di lega d'argento ci sono
5
82 di once di puro argento: poi scrivi le 12 once sotto le
5
85 once, cioè la lega d'argento sotto la lega, come qui si mostra; e moltiplica
5
82 per 12 e dividi per
5
85 e semplifica ciò che può essere semplificato, fanno
3
55 once, e tanto argento puro c'era nella libbra scritta sopra. E sappi che
(PdA)
in questo modo puoi sapere quanto argento puro c’è in qualunque quantità di qualunque bolzonaglia; una volta saputo quanto argento c’è in un’unità di quella bolzonaglia o in un'oncia, o nelle libbre o in qualunque altra quantità.
In dipendenza da verba dicendi e sentiendi, accanto alle infinitive oggettive, sono abituali nel Liber abbaci le dichiarative introdotte da quod o quia (assai diffuse già nel sec. IV d.C. anche nella lingua letteraria), talora costruite con il congiuntivo. [PdA,pag.5]
|
 |
|
Termina la seconda parte dell'ottavo capitolo.
|
|
|