Il calendario civile segnava il 9 agosto del 1173 mentre, secondo il mos pisanus ^[1] Nel calendario pisano l’anno iniziava il 25 Marzo, il giorno dell’Annunciazione e quindi dal primo gennaio al 25 marzo l’anno civile e quello pisano coincidono, dal 25 marzo al 31 dicembre l’anno pisano è avanti di una unità. [3] S. Costanzo, Calendario pisano, Linee infinite edizioni, 2018. , il 25 marzo alle ore 12 di quell’anno si entrava, a Pisa, nel 1174, dunque quel 9 agosto 1174 del calendario pisano, inizia una lunga e affascinante avventura architettonica che durerà quasi due secoli: la costruzione della torre campanaria da affiancare al Duomo.

Sono gli anni settanta del XII secolo, gli anni nei quali si pensa sia nato Leonardo figlio di Bonacci il padre della matematica moderna.

La data è incisa sulla destra all’ingresso della torre:

.

ed è confermata dal cronista Maragone[2] B. Maragone, Gli annales italiani, Forgotten Books. che ci ha lasciato una dettagliata cronaca, indizione per indizione ^[2] L’indizione è un altro modo per stabilire l’anno: il tempo era diviso in cicli di 15 anni ciascuno e l’indizione (da 1 a 15) indicava l’anno all’interno del ciclo.
1153, 1168, 1183, 1198 sono gli anni inziali dei cicli nella seconda metà del XII secolo e l’anno 1173 corrisponde alla sesta indizione del ciclo che iniziava nel 1168. , degli avvenimenti principali della Pisa del XII e XIII secolo:

Maragone ci comunica che il campanile sarà circolare, cosa non inconsueta nei minareti arabi, e che l’edificazione vera e propria inizierà l’anno successivo per lasciare tempo alle fondamenta di stabilizzarsi.

In realtà l’anno prima Berta Bernardi, una nobildonna pisana, aveva lasciato una donazione di 3 Lire (pari a 60 soldi pisani) all’Opera di Santa Maria Maggiore, una grande scuola di architettura, un cantiere permanente collegato con il vicino arsenale navale, responsabile della costruzione del Duomo, all’epoca in via di ampliamento, e del Battistero che si stava completando. La donazione era destinata a comprare le prime pietre per iniziare l’edificazione della torre campanaria del Duomo. Non molto se pensiamo alla grandiosità del progetto che i pisani avevano in mente, ma comunque un incentivo ad iniziare i lavori subito, malgrado la grande difficoltà economica che si viveva a Pisa in quel 1173, come ci racconta lo stesso Maragone[2] B. Maragone, Gli annales italiani, Forgotten Books. . .

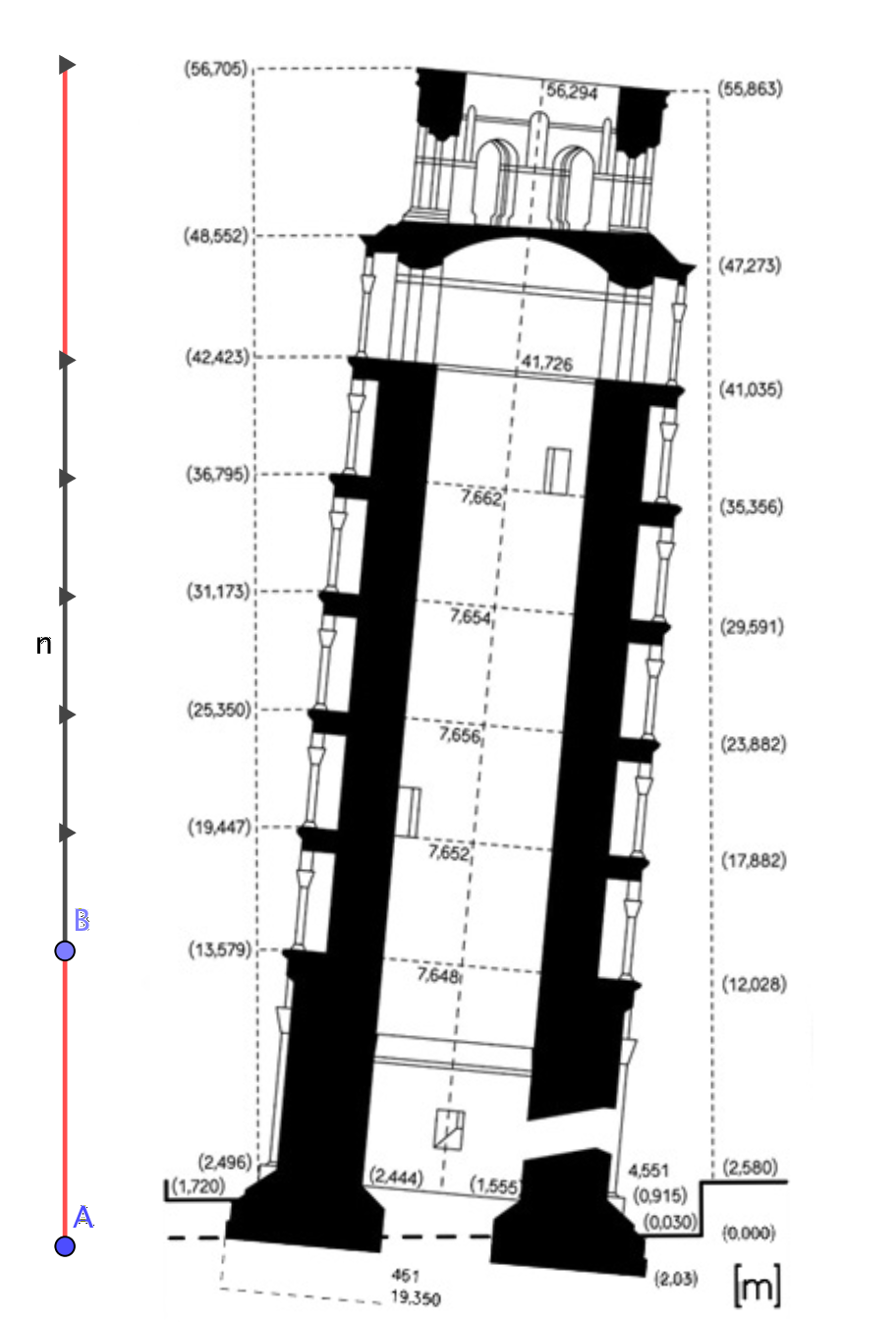
Il grandioso progetto, che si ritiene fosse dell’architetto Diotisalvi di origine palestinese[4] P. Perotti, Breve storia della torre di Pisa ed. Pacini, 2003. , immaginava una torre altissima, di 100 braccia pisane (1 braccio è circa 58,3 cm.) equivalente a 20 pertiche (1 pertica = 5 braccia) o anche a 120 piedi pisani. Le 20 pertiche di altezza erano divise in 7 livelli secondo la successione

Le stesse case torri a Pisa erano dotate di terrazzi e soppalchi in legno esterni alle mura della casa, dove le famiglie si mostravano ai passanti e da dove potevano osservare gli eventi circostanti ed anche difendersi, dall’alto, da eventuali aggressioni nemiche.

La cella campanaria avrebbe dovuto ospitare 6 campane, una per ognuna delle sei note che all’epoca facevano parte della scala musicale: dal Do al La, ma successivamente si pensò di ospitare 12 campane 6 grandi e 6 più piccole per rendere possibile complesse e imponenti armonie musicali.

Infine l’ombra della Torre al solstizio d’inverno, il giorno di Natale all’alba, avrebbe dovuto toccare, e tocca, l’altare maggiore all’interno del Duomo, come segno della nascita di Cristo e dell’inizio, con l’allungarsi delle giornate, della stagione della luce.

Ma la cosa più straordinaria e che, secondo alcuni[4] P. Perotti, Breve storia della torre di Pisa ed. Pacini, 2003. la torre avrebbe potuto essere un gigantesco cannocchiale col quale guardare le stelle anche di giorno. All’ingresso della torre nel buio del cilindro interno, guardando verso l’alto, lo sguardo, attraverso un foro, come una lente, collocato in cima al sesto livello, di diametro inferire al diametro del cilindro, avrebbe potuto vedere le stelle anche di giorno.

Una scultura all’ingresso della torre, in questa incredibile lettura, rappresenterebbe le costellazioni, delle due Orse, del drago e del toro, in transito in quel lembo di cielo, il giorno di Natale. È possibile immaginare che Galileo Galilei abbia potuto, nella sua Pisa, magari bambino, magari per la prima volta, magari per gioco, magari di notte, guardare il cielo con quel gigantesco cannocchiale. Purtroppo nel 1935 si costruì un solaio al primo piano dove collocare gli strumenti necessari al controllo della stabilità della torre e l’effetto oggi è solo una fantastica suggestione.

bassorilievo, duomo parte meridionale

La “firma” di Diotisalvi.
bassorilievo, ingresso della Torre

La realizzazione di questo progetto non fu certo facile e ci vollero circa due secoli e più architetti per portarlo a compimento. Ci sono molte ragioni per ritenere che la costruzione cominciò ad inclinarsi dopo la realizzazione del terzo livello. In una pergamena poco posteriore al 1233 troviamo annotato in calce l’esatta data, 1174, della fondazione del campanile e un piccolo disegno che rappresenta uno schizzo della torre campanaria coi primi tre livelli e una sorta di cupola che ricopre il quarto.

I lavori furono sospesi e non sappiamo come e quando e da chi furono ripresi. Ci sono documenti nei quali troviamo citati vari personaggi nell’atto di impegnarsi a continuare la costruzione della Torre per conto dell’Opera Santa Maria Maggiore: Benenato nel 1233, Guido spadaio nel 1260, Ranieri Vallecchia nel 1270, Orlando Sardella nel 1271. Sicuramente Fibonacci non poté vedere la torre conclusa. Sappiamo di una commissione notarile che nel 1298 misurò con cura la pendenza della torre che probabilmente era arrivata all’ultimo livello.

Ci furono vari progetti per la realizzazione della cella campanaria e finalmente, la posa della campana maggiore, con la quale possiamo ritenere conclusa l’edificazione della Torre, risale al 1373. Antonio Veneziano nell’affresco che rappresenta il funerale di San Ranieri, realizzato all’interno del Campo Santo a Pisa nel 1384-86, oggi fortemente danneggiato, inserisce come compiuta la torre campanaria.

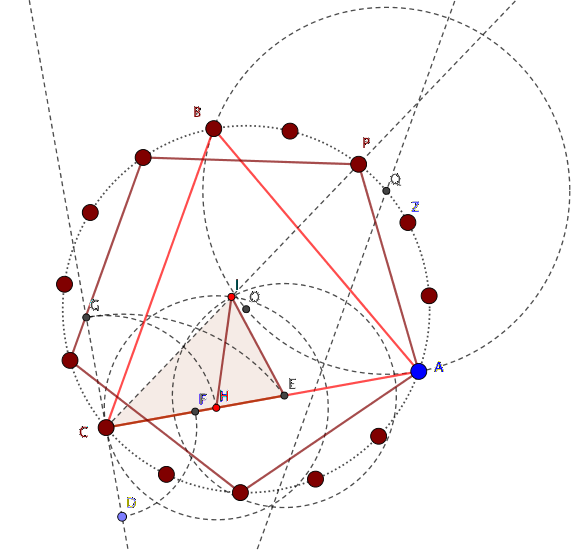
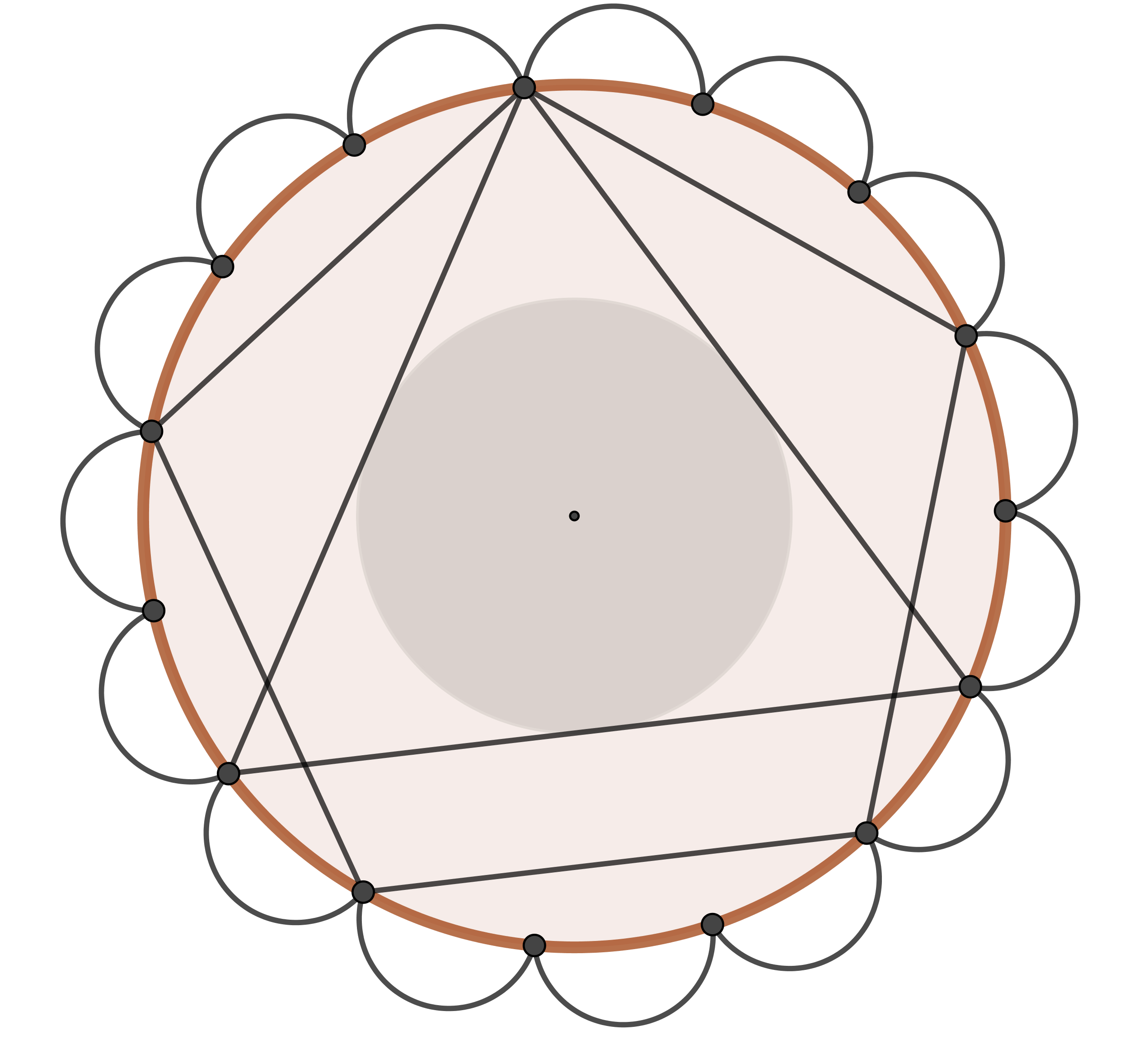
Ma la cosa per noi più interessante, di cui pochi parlano, è il tipo di simmetria scelta. Alla base abbiamo 15 colonne e in ogni loggiato ne abbiamo 30. Il pentadecagono è una figura geometrica rarissima, se non unica, nell’architettura del tempo e molto difficile da costruire con riga e compasso. Per determinate la posizione delle colonne occorre saper dividere esattamente una circonferenza in 15 parti uguali, cosa che Euclide tratta nell’ultima proposizione del IV libro degli elementi dove si insegna a dividere la circonferenza in 3, 4, 5, 6, 15 parti uguali. La divisione in 6 o 3 parti è molto semplice perché il lato dell’esagono regolare è uguale al raggio della circonferenza, possiamo anche facilmente dividere un arco di circonferenza in due parti uguali, costruendo l’asse di un segmento e quindi trovare il modo per dividerlo in 4, 8, 16 parti. La costruzione del pentagono regolare presenta le maggiori difficoltà perché prima si deve saper trovare la sezione aurea di un segmento, poi si deve saper costruire un triangolo isoscele con gli angoli alla base uguali al doppio dell’angolo al vertice e, con questi ingredienti, dividere la circonferenza in 5 parti uguali. Infine la costruzione del pentadecagono si ottiene sovrapponendo la costruzione del triangolo equilatero con quella del pentagono regolare.

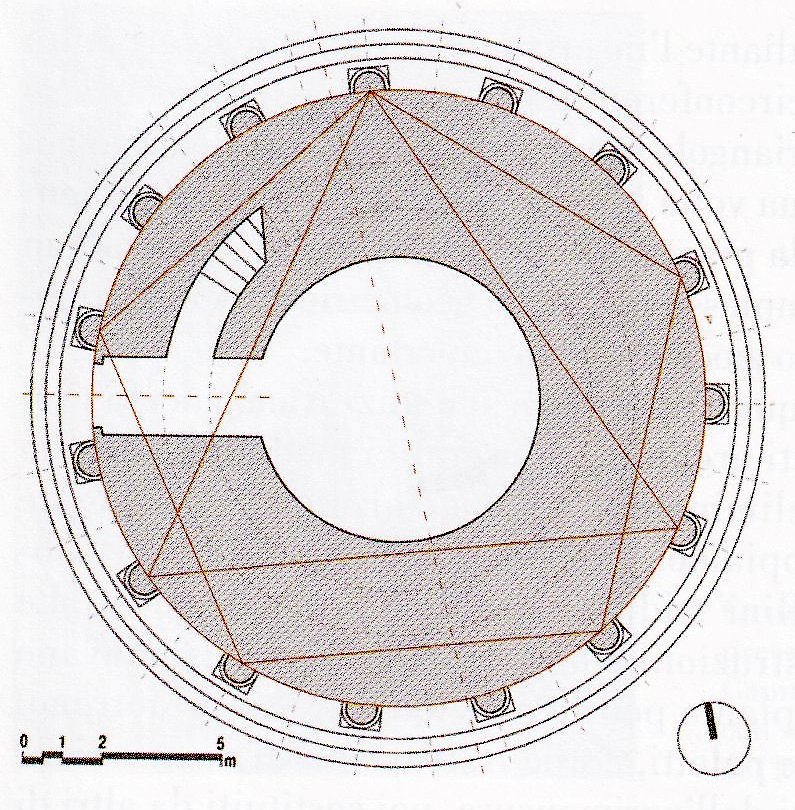
La pianta della torre sembra indicare i passi di questa costruzione: il triangolo equilatero inscritto nella circonferenza definisce l’anello esterno e la circonferenza inscritta in questo triangolo che definisce la base del cilindro vuoto intono al quale si articola la grande scala a chiocciola che sale ai vari loggiati fino alla cella campanaria.

Afferma Valerio Ascani[5] V. Ascani, La torre pendente, Edizioni ETS, 2011.

Perché fu scelto di usare 15 colonne e non 12 (ben più facili da costruire) o 16? Forse per ricordare la festa dell’assunta il 15 Agosto? Non pensiamo che motivi di stabilità possano aver influito la scelta dato che se 15 fosse stato troppo si sarebbe potuto scegliere 12 e se 15 fosse stato poco si sarebbe potuto scegliere 16. Ecco i tre casi messi a confronto

12 colonne

15 colonne

16 colonne

che ci fanno pensare che, da un punto di vista estetico, la differenza sia poco significativa. Secondo il fisico David Speiser[6] D. Speiser,
Matematica araba e pisane nella piazza dei miracoli,
in 'Fibonacci tra arte e scienza', Silvana editore 2002.

Ci piace pensare che questa possa essere la spiegazione: la rivendicazione al mondo intero della forza della cultura matematica nella Pisa del XII secolo, coerente con la grandiosità del progetto di Diotisalvi e con l’impegno e l’orgoglio col quale il progetto, malgrado le enormi difficoltà, fu alla fine portato, senza stravolgimenti, a compimento.

Proponiamo un possibile laboratorio sulla costruzione dei poligoni regolari che si concluda con la costruzione, nel cortile della scuola o in una grande sala, della pianta della torre di Pisa utilizzando al posto del compasso uno spago e più studenti per tener fermo nel punto opportuno il centro del “compasso” e con la corda tesa per tracciare gli archi necessari. Il file GeoGebra allegato suggerisce una possibile costruzione.