L’equazione x3+c = qx2

Franco Ghione

Cominciamo con l’osservare che i matematici arabi avevano inventato degli strumenti per tracciare con continuità una qualunque conica.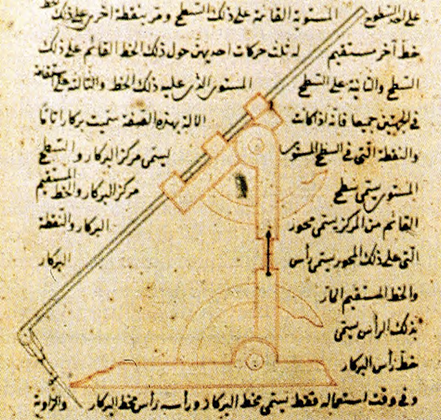
Il più celebre di questi strumenti è il compasso perfetto in grado di tracciare circonferenze, ellissi parabole e iperboli. Un esempio di compasso perfetto è riprodotto nell'immagine sottostante.

Consideriamo l’equazione x3 +  c = q x2.Come prima cosa rendiamo omogenea l’equazione scrivendo il termine noto c come il cubo di un numero p. L’equazione diventa

x3 +  p3 = q x2

e il problema consiste nel trovare un numero x che sostituito nell’equazione produca l’uguaglianza voluta.

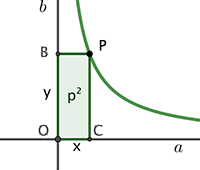
Fissata una unità di misura, tracciamo una iperbole equilatera i cui punti definiscano un’area p2 e che abbia come asintoti le rette perpendicolari a e b e sia O il loro punto di intersezione. Se P à un punto dell’iperbole e B e C le proiezioni ortogonali di P sui suoi due asintoti il rettangolo di lato PB e PC avrà area costante uguale a p2.
Indichiamo per comodità con x la lunghezza, nella data unità di misura, del segmento OC e con y quella del segmento OB; per i punti dell’iperbole sarà dunque xy=p2 o in termini di rapporti

OB : p = p : OC

Consideriamo la parabola che abbia come asse l’asintoto a dell’iperbole precedente, che abbia il vertice nel punto A a una distanza da O uguale al valore del parametro q, e abbia p come lato retto.
Se Q è un qualsiasi punto della parabola e D la sua proiezione ortogonale sull’asse allora, essendo p il suo lato retto, QD2 =pAD. Poiché OA= q abbiamo AD=q-OD e quindi

(q-OD) : QD = QD : p.
OA=q

Se P=Q cioé se l’iperbole e la parabola hanno un punto in comune allora troviamo

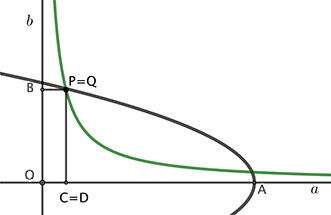
(q-OC) : OB = OB : p = p : OC


Se C=D abbiamo OD=OC=x,
e QD=PC=OB=y
le due relazioni precedenti diventano

(q-x) : y = y : p
y : p = p : x
quindi la misura x del segmento OC risolve l'equazione x3+p3=qx2.

La cosa straordinaria è che la forma geometrica della configurazione formata dalle due curve e dal loro intrecciarsi ci da informazioni algebriche sull’esistenza o meno di soluzioni positive dell'equazione ed anche sul loro valore approssimato.

x3 + 8 = 2x2  (nessuna soluzione) (due soluzioni coincidenti) x3 + 1= 5x2   (due soluzioni >0 distinte)

Infine, se estendiamo la ricerca delle soluzioni anche nel dominio dei numeri negativi, troviamo, per l'equazione x3+p3=qx2 , l’esistenza, comunque siano i coefficienti p e q dell'equazione. di una radice negativa, dato che, per ragioni di continuità e di convessità, la parabola entra sempre nell’iperbole.