progettofibonacci skeda - geometria baratto figura cata

La geometria del baratto: la figura cata

Franco Ghione

La pratica del baratto è certamente la forma più antica di attività commerciale probabilmente sempre esistita e ancora oggi molto praticata. Scambiare alla pari una merce con un'altra ha la caratteristica paradossale di far pensare ad entrambi i soggetti di aver fatto un affare a scapito dell'altro. La cosa può facilmente trasformarsi in un imbroglio ai danni di uno dei due affaristi soprattutto se lo scambio avviene con grandi quantità di merci, provocando liti, cause in tribunale ed altre complicazioni. L'esigenza di matematizzare il baratto, a ciò che niuno sia ingannato, come dice Piero della Francesca nel suo trattato d'abaco, rendendo la transizione in un qualche modo oggettiva diventa una esigenza ineludibile in una economia non più primitiva.

Nella prima parte del capitolo IX Fibonacci stabilisce il modo corretto col quale realizzare delle transizioni commerciali alla pari. Si tratta sempre di grandi quantitativi di merce (centinaia di chili di pepe o di mastice genovese o di cotone da barattare con decine di metri di panno o di seta) il cui commercio non è possibile senza un adeguato apparato matematico e delle regole precise e condivise sulla base delle quali eseguire la transizione. La regola stabilisce che lo scambio è equo se il costo delle due merci è lo stesso, costo che è possibile valutare accordandosi sul prezzo delle due merci. Più in dettaglio, supponiamo di avere due tipologie di merci, ad esempio il cotone e il panno, e di voler barattare una data quantità X di merce del primo tipo con una quantità Y di merce del secondo tipo. Per valutare il costo di X dobbiamo sapere il costo a in lire di una data quantità di merce A del primo tipo, cioè sapere il prezzo v₁ = a/A di quella merce di modo che il costo della quantità X sarà v₁ × X . Ricordiamo che, avendo supposto il costo di una data merce proporzionale alla sua quantità, il costo x della quantità X di merce è tale che:

X =

A = v₁

Analogamente, per valutare il costo di Y, dobbiamo sapere il costo b in lire di una data quantità di merce B del secondo tipo cioè il prezzo v₂ di quella merce. La transizione sarà equa se

v₁ × X = v₂ × Y

cioè

Y =

v₂

v₁ =

Aa ×

Abbiamo questo criterio per stabilire se uno scambio è alla pari: il rapporto tra le quantità di merci scambiato X con Y è uguale al prodotto del rapporto di A con a per b con B.

A =

YB ×

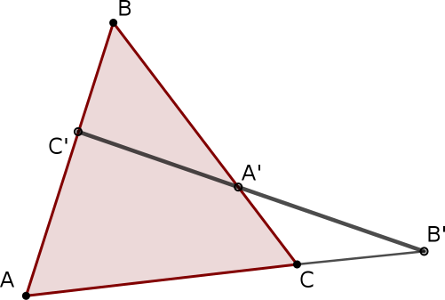
Da un punto di vista geometrico questa considerazione ci porta al teorema di Menelao dove il rapporto composto da due rapporti tra segmenti si realizza con una figura geometrica che gli arabi chiamano la figura Cata e che più avanti descriveremo brevemente.

Nel caso di Fibonacci le grandezze in gioco sono misurate con opportune unità di misura e danno luogo a 6 numeri (interi, rotti o misti) legati dalla relazione

B = Y

Di questi 6 numeri 5 sono conosciuti e uno (X o Y) è incognito.

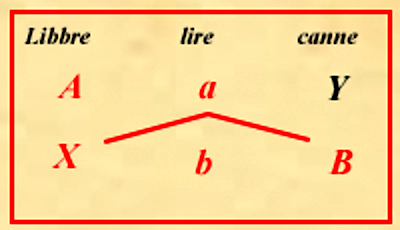
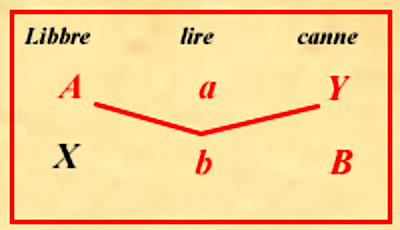
Anche in questo caso Fibonacci introduce un diagramma, una sorta di algoritmo visivo, che permette, una volta disposti correttamente i dati, di trovare la soluzione. I dati sono disposti su 3 colonne e 3 righe. Sulla prima colonna abbiamo l'unità di misura per le merci del primo tipo, la merce A e la merce X , sulla seconda colonna l'unità di misura per i costi, il costo a di A e il costo b di B, sulla terza colonna l'unità di misura per le merci del secondo tipo, la merce B e la merce Y.
Il diagramma non solo compattifica i dati favorendone la memorizzazione visiva, ma indica anche le operazioni da eseguire. Per questo si completa il diagramma con due linee diagonali che congiungono 4 numeri dati, la soluzione del problema si ottiene in ogni caso, sia che si cerchi X che si cerchi Y, moltiplicano i numeri sulle diagonali e dividendo il risultato per il prodotto dei numeri rimanenti proprio perché il prodotto dei numeri sulle due linee spezzate X × a × B e A × b × Y sono uguali. Se, ad esempio, le merci del primo tipo vanno a peso (come il cotone) e quelle del secondo tipo a canne (come il panno) e i costi sono misurati con lire il diagramma (scritto da sinistra a destra) avrà la forma

X × a × B

A × b = Y

A × b × Y

a × B = X

Un caso particolarmente interessante per lo sviluppo di una economia scientifica riguarda il cambio di monete che nel medio evo circolavano ovunque con i più diversi valori, nomi ed equivalenze. Essere in grado di cambiare le monete da un tipo ad un altro in modo scientifico per conto di terzi era una delle nuove attività, probabilmente svolte dai banchieri che si poteva attuare a tavolino alla sola condizione di saper fare calcoli esatti e al di sopra delle opinioni. A partire dal secolo XII venivano coniate monete di diverso valore in ogni centro commerciale. Per citare solo alcune tra quelle che ritroviamo nel Liber abaci, abbiamo monete di Pisa, Lucca, Firenze, Genova, Bologna, Torino, Barcellona, provenzali, per non parlare delle monte arabe, imperiali o bizantine (I denari pisani fino alla prima metà del ‘200).

Denari pisani del XII secolo
Denaro imperiale risalente al tempo di Federico II	Tareno (o tarì ) moneta araba d'oro del XI secolo usata a Palermo anche dopo la dominazione araba)

Il cambio si otteneva sapendo il prezzo delle due monete in monete pisane e usando lo stesso procedimento utilizzato per i baratti.

(IX.1.15) Ugualmente se nello stesso modo si chieda quanti soldi genovesi qualcuno avrà avuto per 7 soldi imperiali; sapendo che 12 soldi imperiali valgono 31 soldi pisani, e 12 soldi genovesi, valgono 22 soldi pisani.

Scriviamo i dati usando il nostro “algoritmo visivo"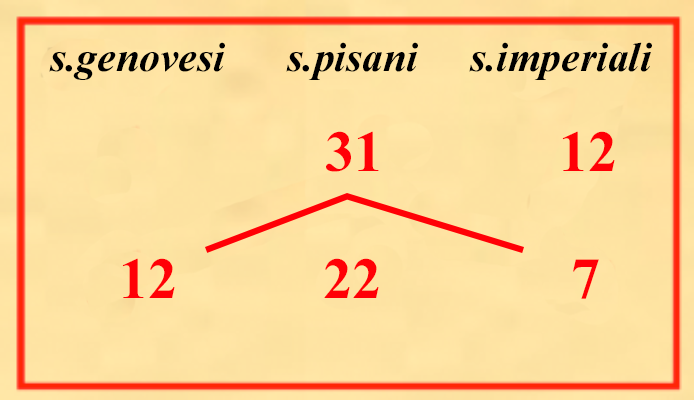

eseguendo il calcolo otteniamo

217

22 = 9

Abbiamo in cambio 9 soldi e

22 di un soldo. Vediamo quanti denari corrispondano i

22 di un soldo, sapendo che 1 soldo equivale a 12 denari. Sviluppando il calcolo otteniamo che

22 di un soldo equivalgono a 10 denari e

11 di denaro. Dunque i 7 soldi imperiali equivalgono a 9 soldi genovesi e 10 denari e

11 cioè poco più di 9 soldi 10 denari e

3 di denaro che nella scrittura di Fibonacci diventa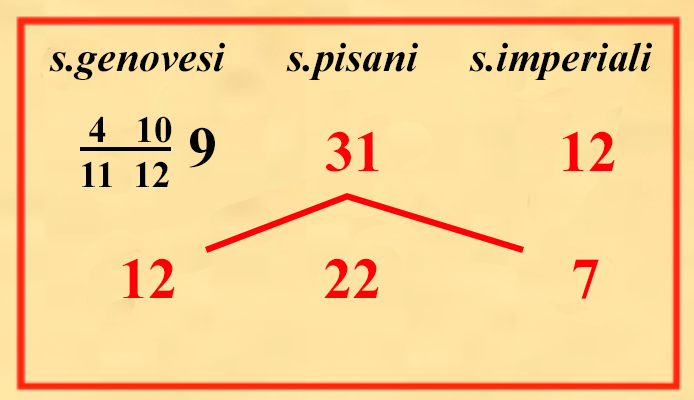

Il calcolo esatto della divisione, tendo conto del resto di

11 di un denaro, anche se questa “somma” non è eseguibile non essendoci moneta più piccola del denaro, permette di avere una rendicontazione precisa del cambio effettuato che, se per il singolo individuo che ha cambiato i suoi soldi imperiali in soldi genovesi non ha importanza, costituisce per il banchiere un minimo guadagno che diventa consistente col crescere delle operazioni di cambio effettuate. Si profila così un nuovo impiego che produce ricchezza prefigurando le prime forme di mercato valutario. Il listino dei cambi è ovviamente in continuo movimento seguendo l'andamento dell'inflazione cosa che richiede una certa expertise nel nuovo calcolo che ogni volta si ripresenta con altri valori. In Fibonacci nei paragrafi seguenti il paragrafo (IX.1.15) che abbiamo citato, troviamo diversi casi nei quali il valore del soldo imperiale passa da 31 denari pisani (IX.1.15) a 31

2 (IX.1.19) a 32

4 (IX.1.17) a 33

4 (IX.1.18) e, mentre il soldo pisano si andava svalutando rispetto a quello imperiale, il suo valore saliva invece rispetto al soldo genovese passando da un valore di 22 denari pisani per un soldo genovese a 21

3 a 19

4.
Le cose sono ovviamente molto complicate dalla presenza sempre crescente di nuove monete locali al punto da richiedere una nuova tipologia di scuola capace di formare le emergenti classi dominanti a questa nuova rapidissima trasformazione economica della società. Le nuove scuole d'abaco avranno questa funzione ma anche, mettendo la matematica e i suoi algoritmi di calciolo al centro della formazione dei giovani, la funzione di sviluppare la matematica come scienza astratta, come forma di pensiero originale funzionale non solo all'economia ma allo sviluppo di qualsiasi scienza quantitativa.

I problemi bilineari

La teoria del baratto che abbiamo esposto si basa sul fatto che il costo di una merce è legato alla sua quantità da una relazione lineare: il costo di una quantità A di una data merce (misurata con una fissata unità di misura) è dato da

F(A) = v A

dove v = F(1) è il prezzo di quella merce cioè il suo costo unitario. La relazione che lega la quantità di merce al suo costo è dunque lineare. Vi sono in Fibonacci interessanti problemi per i quali una data grandezza dipende linearmente da due variabili indipendenti che abbiamo chiamato bilineari e che, da un punto di vista geometrico, riportano alla figura Cata.
Ecco il primo esempio:

(IX.3.1) Cinque cavalli mangiano 6 sestari ^[NdT]
Il sestario è una antica unità di misura di volume.
di orzo in 9 giorni; si chiede in quanti giorni, in questo modo, dieci cavalli mangeranno 16 sestari

Consideriamo la relazione P(a,b) che indica la quantità di orzo (misurato in sestari) che a cavalli mangiano in b giorni. E' ragionevole pensare, se le cose procedono in questo modo, che P(2a,b) = 2P(a,b) e P(3a,b) = 3P(a,b) ecc, cioè che, tenendo fisso il numero dei giorni b, la relazione conservi i multipli e quindi sia lineare nella prima variabile. Se a e x sono numeri interi (che indicano il numero dei cavalli considerati) abbiamo allora

P(a,b)

P(x,b) =

e quindi, per a=1, P(x,b) = P(1,b)x dove P(1,b) è la quantità di orzo che un cavallo mangia in b giorni. Ugualmente fissato a, è naturale pensare che P(a,2b) = 2P(a,b) e P(a,3b) = 3P(a,b) ecc, cioè che tenendo fisso il numero di cavalli e raddoppiando il numero dei giorni raddoppi anche la quantità di cibo consumata, triplicando triplichi ecc. E' ragionevole pensare quindi che, se le cose procedono in questo modo, P(a,b) sia lineare anche nella seconda variabile b. Per questo diciamo che la relazione P(a,b) è bilineare. Se b e y sono numeri che indicano numero di giorni o loro frazioni abbiamo:

P(a,y)

P(a,b) =

e quindi, per b=1, P(a,y) = P(a,1)y dove P(a,1) è la quantità di orzo che a cavalli mangiano in un giorno. Mettendo insieme le due relazioni troviamo l'espressione analitica della funzione P:

P(x,y) = P(x,1) y = P(1,1) xy = μ x y.

Dove μ indica la quantità di orzo che 1 cavallo mangia in un giorno. Fibonacci, riesce a ridurre il problema che abbiamo detto e altri a lui simili a un problema analogo a un problema di baratto: consiglia di scrivere

Poiché P(a,b) = μ ab e P(x,y) = μ xy abbiamo

P(a,b)

ab =

P(x,y)

xy e dunque i prodotti sulle due spezzate diagonali ovvero a × P(x,y) × b

x × P(a,b) × y coincidono e possiamo, anche in questi casi, applicare il nostro “algoritmo visivo” per risolvere il problema proposto. Ma di più, lo stesso schema ci fornisce la soluzione anche a problemi ottenuti cambiando i dati a piacimento. Ad esempio se ci poniamo la domanda seguente:

5 cavalli mangiano 6 sestari in 9 giorni quanti cavalli mangiano 16 sestari in 12 giorni?

la soluzione è scritta nel diagramma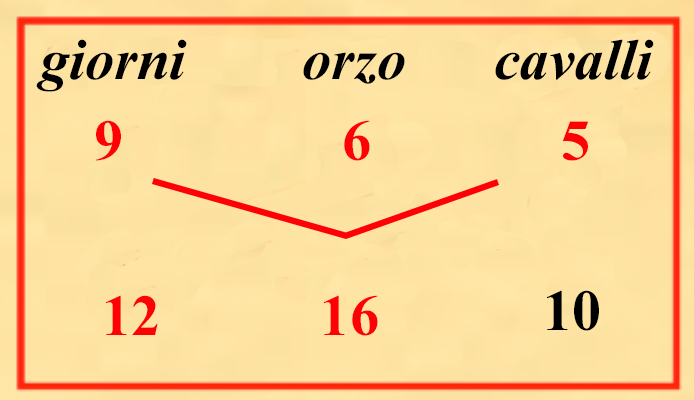

(9 × 16 × 5)

(12 × 6) = 10

Un problema della stessa natura è il problema (IX.3.8) con le sue varianti:

In una certa pianura un certo re mandò 30 uomini per piantarvi alberi, questi piantarono là 1000 alberi in 9 giorni; e si chiede in quanti giorni 36 uomini avrebbero piantato 4400 alberi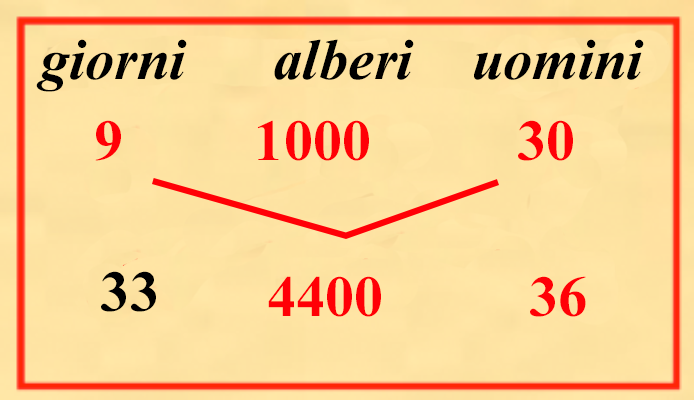

(9 × 4400 × 30)

(1000 × 36) = 33

in 33 giorni 36 uomini avrebbero piantato 4400 alberi.

Vi sono due varianti allo stesso problema a seconda dei dati conosciuti.

Prima variante:
In una certa pianura un certo re mandò 30 uomini per piantarvi alberi, questi piantarono là 1000 alberi in 9 giorni, quanti alberi avrebbero piantato 36 uomini in 33 giorni

Seconda variante
In una certa pianura un certo re mandò 30 uomini per piantarvi alberi, questi piantarono là 1000 alberi in 9 giorni, quanti uomini avrebbero piantato 4400 alberi in 33 giorni

Ecco un ulteriore problema bilineare che dimostra l'importanza in tutti i tempi del vino!

Cinque uomini mangiano 4 moggi ^[NdT]
Il moggio è una antica unità di misura di volume di origine romana corrispondente a circa 9 litri
di frumento in un mese, cioè in 30 giorni. Quindi altri sette uomini chiedono di sapere, quanti moggi saranno necessari, nello stesso modo, negli stessi 30 giorni.... E sappi perché abbiamo proposto questo problema; perché spesso tra i mercanti sorge il problema anche sul vino che si beve; perciò tienilo tenacemente in memoria, in modo da saperci lavorare in casi simili.

(30 × 4 × 7)

(30 × 5) = 5

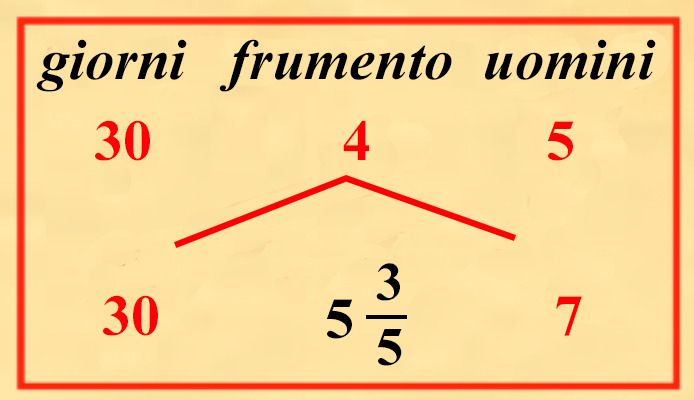Attenzione agli algoritmi

In questi problemi e in altri che coinvolgono entità che non si possono “rompere” (cavalli, uomini ecc) la soluzione va espressa in numeri interi e non rotti: ne segue una discussione ulteriore sui numeri che si trovano e su quale sia la migliore soluzione con numeri interi. In definitiva non solo l'impostazione del problema, le ipotesi alla base del modello e gli strumenti matematici utilizzati richiedono una riflessione critica ma anche il risultato ottenuto va discusso tornando al problema iniziale senza accettare ciecamente il risultato dell'algoritmo che potrebbe portare al dimezzamento di un uomo! E' essenziale rendersi conto del fatto che la soluzione fornita dall'algoritmo può essere messa in discussione prima di tutto confrontandola con la realtà e, in secondo luogo essendo ben consapevoli delle ipotesi che lo giustificano. Proprio questo secondo momento che ci viene spesso nascosto. In una società come quella attuale dominata da algoritmi spesso molto complessi coi quali vengono fatte valutazioni e scelte che incidono profondamente sulla vita delle persone, come la propria affidabilità creditizia o la propria efficacia come ricercatore o come insegnante, sarebbe essenziale che anziché affidarsi ciecamente ai risultati di questi algoritmi, si discutano le ipotesi con le quali sono stati realizzati e si confrontino i risultati forniti con la realtà.

La figura Cata

I problemi sui baratti e quelli che abbiamo chiamato bilineari hanno un interessante corrispondente geometrico nel teorema di Menelao d'Alessandria (I-II sec. d.C.) che permette una soluzione di tipo euclideo: cioè realizzando una figura con riga e compasso. Questo teorema, per le sue importanti applicazioni astronomiche è citato nell'Almagest di Tolomeo, ma la sua versione originale si trova nella Spherica di Menelao, opera in tre libri, nei quali si espone la geometria intrinseca della sfera dove il teorema è esposto nella sua versione sferica. Questo testo è pervenuto fino a noi solo nella sua traduzione araba poi rivista da Maurolico nel XVI secolo e dall'astronomo Halley nel XVIII. Fibonacci, cita il teorema di Menelao col nome di figura Cata (in arabo Kata significa taglio, taglierino), e deve averne studiato le proprietà durante la sua formazione scientifica con i maestri arabi perché ne parla ampiamente nella sua Pratica geometrica [BB]

B. Boncompagni,
Scritti di Leonardo Pisano,vol II, pg. 53-55

. Questo teorema permette di interpretare geometricamente il rapporto composto tra due dati rapporti. Anche se non troviamo negli elementi di Euclide una esplicita definizione di rapporto composto possiamo capire di cosa si tratti vedendo come questa nozione venga utilizzata in alcune proposizioni degli Elementi. Ad esempio la proposizione 23 del VI libro afferma che due parallelogrammi simili stanno tra loro come il rapporto composto dal rapporto tra i lati

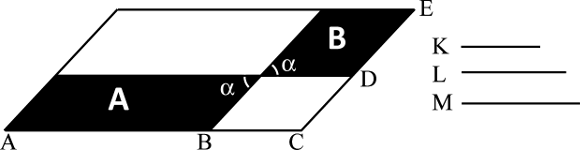
Per specificare cosa si debba intendere per rapporto composto di AB : BC con CD : DE, Euclide introduce un segmento K (arbitrario) e considera il segmento L unicamente individuato come quarto proporzionale dalla proporzione AB : BC = K : L e il segmento M unicamente individuato dalla proporzione CD : DE = L : M. Fatto questo, Euclide dimostra che, indipendentemente da come si sia scelto K, il rapporto tra le aree è sempre dato da K : M. Il rapporto composto di K : L con L:M è dunque per definizione il rapporto K : M e in generale, dati due rapporti qualsiasi, usando l'esistenza e l'unicità del quarto proporzionale, ci si riduce a questo caso. Ovviamente si dovrebbe dimostrare che il rapporto K : M non dipende dalla scelta di K. Da un punto di vista numerico, introducendo una unità di misura per i segmenti, e indicando con lettere corsive le corrispondenti misure dei segmenti, il rapporto composto si riduce al prodotto tra i due rapporti dato che

L ×

M =

La figura Cata permette di costruire geometricamente con riga e compasso il rapporto composto che passando alle rispettive misure si calcola eseguendo semplicemente i prodotti dei numeratori e dei denominatori dei due rapporti.


Consideriamo un segmento AB e un suo punto P che definisce il rapporto AB : AP
	AB : AP = 6 : 5
e un segmento CD e un suo punto Q che definisce il rapporto CD : CQ
		CD : CQ = 4 : 3

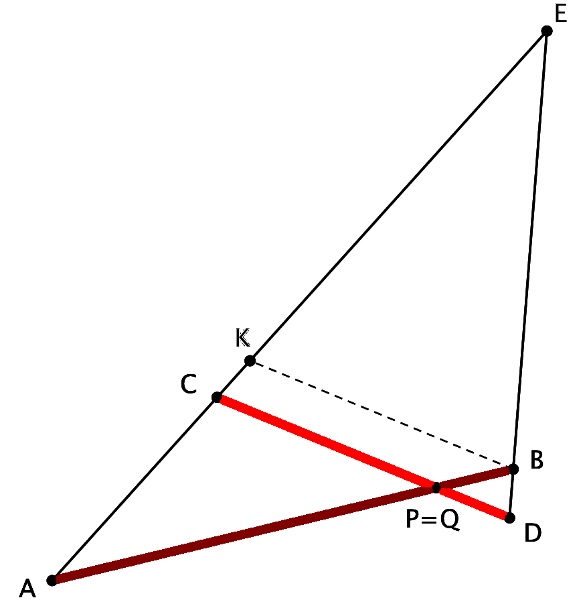
il teorema di Menelao nella sua versione piana, permette di costruire con riga e compasso un segmento EF e un punto X su EF tale che il rapporto EF : EX sia il rapporto composto di AB : AP con CQ : CD, cioè, nel caso dell'esempio il rapporto

5 ×

4 =

	La figura Cata si costruisce nel modo seguente: si identificano i punti P e Q in un unico punto e si tracciano le rette AC e BD. Queste rette sono parallele se e solo se AB : AP = CD : CQ, quindi se i rapporti sono diversi le rette si incontrano in un punto E e si può dimostrare che EB : ED è il rapporto composto di AB : AP con CQ : CD.
	Infatti, tracciato la BK parallela a CD, abbiamo AB : AP = KB : CQ (AKB simile a ACQ)
	KB : CQ composto con CQ : CD = KB : CD
	quindi AB : AP composto con CQ : CD = KB : CD
	ma KB : CD = EB : ED (KBE simile CDE) AB : AP composto con CQ : CD = EB : ED
6 5 × 3 4 = 18 20 = EB : ED

Fissata una unità di misura per i segmenti indichiamo con A la misura di AB, con a < A la misura di AP, con B la misura di CD e con b < B quella di CQ e, infine, con X la misura di DE e con x < X quella di EB, il teorema che abbiamo dimostrato ci dice che

a ×

B =

cioè che X

B = A

x. Abbiamo dunque due gruppi di 3 numeri, X, a, B e A, b, x legati da una relazione che ci permette di ricavare 18 altri enunciati esprimendo il rapporto di un numero del primo gruppo con un numero del secondo gruppo come rapporto composto con i rimanenti numeri ad esempio o anche ognuna delle quali può essere interpretata geometricamente riferendosi alla figura Cata.
Vi sono anche diverse figure a seconda di come siano i due dati rapporti se minori di 1 o maggiori e sembra che gli arabi abbiano esaminato da un punto di vista combinatorio queste 18 possibilità e le diverse figure alle quali danno luogo.
Tutto questo permette di esprimere geometricamente, nei problemi bilineari la soluzione del problema sia che l'incognita del problema sia x, y o P(x,y) come nei tre casi che abbiamo illustrato.

Un enunciato univoco del teorema di Menelao piano che comprende ogni caso possibile è il seguente:

Teorema di Menelao piano

Sia dato un triangolo A, B, C e una trasversale che non passa per i vertici del triangolo; tale retta interseca nei punti A', B' ,C' le rette per BC, CA e AB rispettivamente, allora il rapporto composto di AC' : C'B con BA' : A'C è uguale al rapporto B'A : CB' e, passando alle misure dei segmenti (indicate con lettere corsive) abbiamo

AC'

C'B ×

BA'

A'C =

B'A

CB'

Notiamo che se la trasversale che taglia il triangolo tende a essere parallela alla base AC allora il rapporto a secondo membro tende a 1 e il teorema si riduce al teorema di Talete (Elementi, VI, 2). La dimostrazione usa la teoria euclidea della similitudine: si traccia la parallela BH al lato AC del triangolo: i triangoli HBC' e AC'B' sono simili e anche i triangoli A'BH e A'CB' sono simili quindi abbiamo le uguaglianze di rapporti euclidei


AC’ : C’B = B’A : BH	BA’ : A’C = BH : CB’

Ne segue che il rapporto composto di AC’ : C’B con BA’ : A’C è uguale al rapporto composto di B’A : BH con BH : CB’ ma ora questo rapporto per come è stato definito è proprio B’A : CB’.

E’ interessante osservare che il rapporto composto veniva interpretato, prima di Fibonacci più come una “somma” di rapporti che come “prodotto” cosa che ritroviamo ancora oggi nella teoria musicale degli intervalli. Un intervallo di quinta, sul pianoforte, si ottiene contando 5 tasti bianchi, ad esempio DO₁-SOL e corrisponde a un rapporto tra le frequenze di 3 : 2 mentre un intervallo di quarta contando 4 tasti bianchi ed esempio SOL-DO₂ e corrisponde a una rapporto tra le frequenze di 4 : 3. Il rapporto composto di 3 : 2 con 4 : 3 corrisponde al rapporto composto di 6:4 con 4 : 3 che, per definizione di rapporto composto, coincide con 6 : 3 = 2 : 1 dunque la composizione dei due rapporti DO₁-SOL con SOL-DO₂ è il rapporto di ottava DO₁- DO₂ ottenuto contando 5 + 4 - 1 = 8 tasti bianchi (-1 perché il SOL è contato due volte).
Questa interpretazione del rapporto composto come somma si riscontra anche nell’operazione inversa che oggi consiste nella divisione di due rapporti mentre anticamente era intesa come rimozione di un rapporto da un altro, parola che fa pensare a una sottrazione più che a una divisione. Nel Liber abaci (IX.2.17) Fibonacci spiega come realizzare il rapporto composto di più rapporti (non solo due) eseguendo semplicemente il prodotto dei numeratori coi denominatori e l’antica operazione di rimozione che lui chiama estrazione di una frazione da un’altra ( extrahere ) diventa, in questo conteso, l’operazione inversa alla moltiplicazione, cioè la divisione. Ogni cosa rientra nella naturale armonia della nuova aritmetica dei numeri misti.