
Inizia la settima differenza delle regole pertinenti alla messa in lega.
|
||
| (XI.7.1 ; G: XI.131) Un uomo taglia due pezzi d'oro il cui peso totale era di una libbra; di questi ne vende uno a 67 bizanti per libbra; e l'altro invece a 50 bizanti per libbra, ebbe 56 bizanti per entrambi i pezzi; si chiede quanto fu il peso di ciascun pezzo. Riportiamo la procedura di questo problema alla cultura delle monete. Come se si dicesse: ho moneta da 67 once, e da 50; e voglio ricavare da esse moneta da 56; in questo metodo si è mostrato che si fa così: la differenza che c'è da 50 a 56, cioè 6, si pone sopra il 67; e la differenza che c'è da 56 a 67, cioè 11, si pone sopra il 50; si somma il 6 con l'11, fa 17; e si moltiplica il 6 e l'11 per il 12, cioè per la quantità di once di ciascun pezzo, e si dividono entrambe le moltiplicazioni per 17, farà 4174 once come peso del pezzo più alto; e 13177 once come peso del pezzo più basso. | 67x1+50x2 = 56(x1+x2)
x1+x2 = 12

|
|
Ancora sull'uomo che ha ricavato 2 pezzi d'oro.
|
||
|
(XI.7.2 ; G: XI.133)
Se poi si dicesse che quei due pezzi pesano 11 once; e si vendano ugualmente a 56 bizanti, si dovrà fare così: come se si dicesse: poiché 11 once valgono 56 bizanti; quanto valgono allora 12 once, cioè una libbra: si moltiplica 12 per 56, fa 672: si divide per 11, fa
11161 bizanti. Ora si può dire: ho moneta da 67, once e da 50; e voglio fare moneta da
11161; e si farà dopo in base al modo detto. Ugualmente se quei pezzi pesassero 13 once, si moltiplica similmente 12 per 56, e si divide per 13, fa 91351; e si può dire allora: ho moneta da 50, e da 67, e voglio fare moneta da 91351 once, e così puoi fare nel caso di tre o più pezzi. Però fa sempre in modo che il prezzo di tutti i pezzi sia riportato alla quantità di quella vendita come abbiamo fatto per i pezzi precedenti. Quando, posto che quei due pezzi fossero da 11 once, o 13, li abbiamo riportati alla quantità del prezzo di una libbra; poiché della libbra fu detto che valeva 50 e 67 bizanti. |

|
|
Su un uomo che compra 7 libbre di tre carni per 7 denari.
|
||
pg.160 |
(XI.7.3 ; G: XI.135) Un tale comprò carne di maiale per 3 denari la libbra, e di mucca per 2 denari; e anche di cinghiale per 12 denaro; e con quelle tre carni ebbe 7 libbre per 7 denari; si chiede, quanto ebbe di ciascuna: poiché con quelle tre carni per 7 denari ebbe 7 libbre di carni, allora 1 libbra vale 1 denaro: perciò ho moneta da 3, e da 2, e da 12; e voglio fare moneta da 1: che si faccia secondo l'insegnamento detto sopra, cioè somma 2 con 3, farà 5: poni la differenza che c'è fra 1 fino alla metà di questo 5 sopra 12; e la differenza che c'è da 12 fino a 1, cioè 12 , dividila per 2, farà 14, ponilo sopra il 2; e l'altro 14 ponilo sopra il 3, e somma questi due quarti con il 121 scritto sopra, farà 2: e moltiplica 7 per 121, farà 1210, dividilo per 2, farà 145; e tante sono le libbre comprate di carne di cinghiale. Ugualmente 14, che è posto sopra il 2; o lo stesso che è posto sopra il 3, moltiplicalo per 7, e dividilo per 2, farà 78 di una libbra; e tanto compra di ciascuna delle restanti carni. E se vorrai avere quantità differenti di ciascuna carne nella prescritta spesa, poni di comprare a piacere 1 libbra di carne di maiale per 3 denari, restano 6 libbre delle due carni rimanenti per 4 denari; ciascuna delle quali carni vale 23 di un denaro. Perciò puoi dire: ho moneta da 2 e da 12; e voglio fare 6 libbre di moneta da 23: se con l'insegnamento dato saprai farlo, troverai che di carne bovina ne compra 23 di una libbra per 131 denaro, e di carne di cinghiale 135 libbre per 232 denari, e così ha 7 libbre di carni per 7 denari, come è richiesto. |
3 x1 + 2 x2 +
12 x3 = 7
x1 + x2 + x3 = 7 x1 = x2 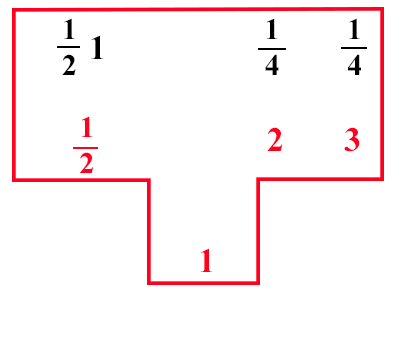
x1 = 1
|
Sulla donna commerciante che compra mele e pere.
|
||
| (XI.7.4 ; G: XI.139) Ugualmente una donna commerciante compra 7 mele per 1 denaro; e ne vende 6 per 1 denaro; e compra 8 pere per 1 denaro; e ne vende 9 [ per 1 denaro ], e spese 10 denari; e ne guadagnò 1; si chiede quanto spese in mele e quanto in pere: così si deve fare, se si suppone che ella spese in mele quei 10 denari, moltiplica 7 per 10, faranno 70 mele; poiché ne ha vendute 6 per 1 denaro, dividi 70 per 6, fa 2311 denari: la stessa cosa fai con le pere, supponendo di investire in esse i 10 denari; e vedrai quante pere avrai di lì: moltiplica dunque 8 per 10, e dividi per 9, fa 898 denari; e puoi dire: ho moneta da 2311 e da 898; e vorrei farne da 11, cioè la somma del profitto e del capitale, poni sopra 2311, secondo l'insegnamento scritto sopra, la differenza che c'è da 898 a 11, cioè 192. E viceversa scrivi sopra 898 la differenza che c'è tra 11 e 2311, cioè 23 [ moltiplica per 9 ] e somma il 6 con il 19; farà 25; e moltiplica 10 per 19, e dividi per 25, fa 357 denari; e tanto mise in pere. | x1 denari investiti in mele x2 denari investiti in pere x1 + x2 = 10 76 x1 + 89 x2 = 1110 (x1 + x2) 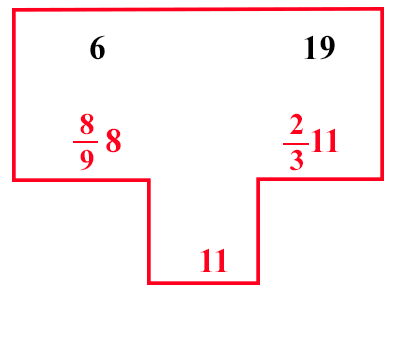
|
|
Su un operaio che lavora in qualche attività.
|
||
pg.161 |
(XI.7.5 ; G: XI.142)
Un operaio [ sapeva che ] avrebbe ricevuto 7 bizanti al mese per il suo lavoro
[NdT]
Si intende che ogni giorno lavorativo guadagna
730 bizanti e ogni giorno di assenza paga una penale di
430 bizanti
; e se per qualche tempo avesse cessato di lavorare, avrebbe dovuto restituire 4 bizanti per la parte di mese [ corrispondente ]; rimase per un mese, nel quale a volte lavorò e a volte no; perciò ebbe 1 bizante per il tempo in cui lavorò, tolto quello in cui non lavorò. Si chiede quanto lavorò, e quanto no in quel mese: farai così. Somma i giorni del mese, che sono 30, con i 7 bizanti, che avrebbe guadagnato, fa 37; e dallo stesso 30 sottrai i 4, che avrebbe restituito se non avesse lavorato: rimangono 26. Ugualmente somma con il 30 il profitto che fece, cioè 1, farà 31; e puoi dire: ho moneta da 26 e da 37; e voglio fare da esse 30 libbre, cioè per i giorni del mese che sono 30, a 31: questo è da fare nel modo detto sopra, cioè porrai la differenza che c'è tra 37 e 31, cioè 6, sopra il 26; e la differenza che c'è tra 26 e 31: cioè 5, ponila sopra il 37: da qui appare chiaramente che lavorò per 5 parti di quel mese e per 6 parti di mese smise di lavorare. Dunque bisogna dividere i giorni del mese, cioè 30, in quelle parti nel modo delle società commerciali, cioè sommi il 5 con il 6, fa 11; per questo 11 dividi la moltiplicazione di 5 per 30, fa
71113 giorni e tanti giorni ha lavorato quell'uomo: similmente moltiplica 6 per 30, dividi per 11, fanno
41116 giorni, nei quali l'uomo menzionato non ha lavorato.
|
x1 giorni lavorativi x2 giorni di assenza x1 + x2 = 30 730 x1 - 430 x2 = 1 Fibonacci riduce a monete (30 + 7) x1 + (30-4) x2 = 31 (x1 + x2) 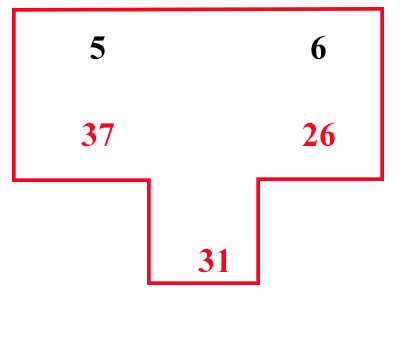
|
|
(XI.7.6 ; G: XI.145)
Ho diviso il 20 in due parti, ho preso 13 di una e
18 di un'altra e li ho sommati al 20; e dalla somma composta ho tolto la quinta parte, è rimasto 20; visto che da qualunque somma si tolga
15 ne restano
45, 20 rappresenta i
45 della somma fatta: visto che
15 di qualunque somma è la quarta parte di
45, allora
15 della somma realizzata è
14 di
45: questo
14 fu
13 della prima parte e
18 della seconda: compreso questo, poni che il 20 sia diviso [ in due parti ] con 20 e con 0; se prenderai
13 della prima parte e
18 della seconda, farà solo
13 di tutto. Se poi prenderai
13 della seconda parte, cioè di 0, e
18 della prima, farà
18 di 20: ma prendendo
13 di una delle due parti richieste, e
18 dell'altra, farà
14 di 20: quindi ho moneta da
13 di 20 e da
18 di 20; e voglio fare moneta da
14 di 20; essendo queste parti di uno stesso numero, cioè di 20, possiamo dire indifferentemente: ho moneta da
13 e da
18 e voglio fare moneta da
14, cioè: ho moneta da 8, e da 3; e voglio fare 20 libbre da 6, permuta le differenze e avrai che la prima parte è
35 di 20, cioè 12, la seconda
25, cioè 8. E se si vuole che resti 19, dalla somma fatta sottrai
15, somma a 19 la sua quarta parte, fa
3423, che è la somma fatta: da questa sottrai 20, resta
343; denominalo a 20, cioè dividilo per 20, farà
316; e allo stesso modo hai moneta da
13 e da
18; e vuoi fare 20 libbre da
316, cioè: ho moneta da 16 e da 6; e voglio fare 20 libbre da 9: scambiate allora le differenze, troverai che la prima parte è
310 di 20, cioè 6; la seconda
710, cioè 14. Ugualmente ho diviso il 20 in tre parti e ad esso sommai 17 della prima parte, e della seconda, e 18 della terza; e dalla somma avuta ho sottratto la sua sesta parte, ed è rimasto 20: e così per quanto è stato mostrato sopra, si troverà che 16 di tutta la somma è 15 dei suoi 56, cioè di 20: quindi hai moneta da 13 e da 17 e da 18; e vuoi fare moneta da 15: posto il problema, potrai ricavare nel modo detto prima le prescritte parti; e la seconda parte starà con la terza in qualunque proporzione vorrai. |
x1 + x2 = 20 13 x1 + 18 x2 = A 45 (20 + A) = 20 13 x1 + 18 x2 = 14 (x1 + x2) 
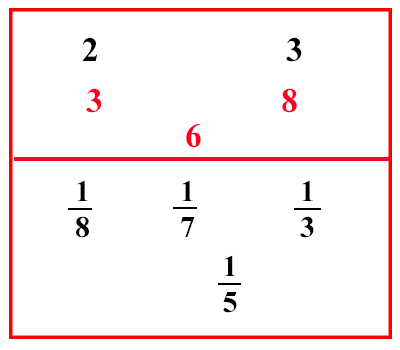
|
|
|
Di un uomo che compra 90 moggi di biade
(PdA)
.
Il testo di Fibonacci parla di monete e di misure, ma anche di mercanzie, di oggetti maneggiati e di luoghi praticati dai commercianti del tempo. Il vocabolario della lingua quotidiana si evolve costantemente introducendo nuovi termini ogni volta che se ne presenti la necessità. Gli antichi Romani conducevano al pascolo (pabulum) gli animali, che mangiavano l’avena, termine atto a designare propriamente una pianta della famiglia delle graminacee. Per indicare le messi mature (messis indica genericamente il raccolto) usavano il plurale fruges (raro il sing. frux), caduto in disuso probabilmente perché suonava troppo vicino a fructus. Perciò il latino medievale introdusse blada (it. biada) dal francone blad. Sappiamo che nella denominazione di blad(a)e rientravano almeno frumentum, milium, fab(a)e, (h)ordeum, lenticul(a)e. [PdA,pag.7]
|
||
| pg.162 | (XI.7.7 ; G: XI.149) Un tale compra a Costantinopoli 90 moggi tra frumento, miglio, fave, orzo, e lenticchie per 1421 bizanti. Ora tenendo conto che cento moggi di frumento erano venduti per 29 bizanti; di orzo invece per 25 bizanti; di miglio poi per 22 bizanti; e di fave ancora per 18 bizanti, e di lenticchie per 16 bizanti, si chiede quanto compra di ciascuna biada; farai così: vedi quanto valgono 100 moggi di biade miste, quando 90 moggi di esse valgono 1421 bizanti. Per saperlo, moltiplica i 100 moggi per 1421 bizanti e dividi per 90, farà 111823 bizanti come prezzo di cento moggi. Perciò per riportare questo problema al modo della messa in lega delle monete, si deve dire: ho monete da 29 once, e da 25, e da 22, e da 18, e da 16; e da esse voglio fare moneta da 111823 once, e fare di essa 90 libre in lega: perciò scrivi il problema in questo modo, e somma insieme il prezzo della biada più cara, cioè i 29 bizanti, con i 25 bizanti, fa 54: e poiché hai sommato insieme due biade, dividi il 54 per 2, fa 27 da cui sottrai 111823 bizanti, restano 7183 bizanti; questo numero è la proporzione di miglio tra le tre biade: perciò dividi 7183 per queste 3 biade, farà 7541; ponilo sopra i 22 bizanti, e sopra il 18, e sopra il 16, come si mostra nel riquadro; e somma insieme il prezzo delle altre tre biade, cioè 22, e 18, e 16, farà 56; dividilo per 3, farà 2318, dal quale fino a 111823 mancano 17184 che è la porzione delle biade più care. Perciò dividi 17184 per 2, farà 17362, ponilo sopra il 29, e sopra il 25: scritti questi così, riporta questo problema ai problemi delle società; cioè uno mise 17362, e un altro altrettanto, e un terzo 7541, e un quarto e un quinto altrettanto; e si sono guadagnati 90 moggi. Per cui conviene che tu faccia da ciascun numero cento ottavi; perché nel 108 sono contenuti i suddetti rotti: e scrivi ciascuno di essi sopra il proprio numero e così avrai 267 sopra il 29 e il 25, e 122 sopra il 22, e il 18, e sopra il 16: una volta sommati insieme, cioè 267, più 267, più 122, più 122, più 122, farà 900; dividi per la loro regola la moltiplicazione dei 90 moggi per ciascuno dei numeri suddetti. O poiché 90 è 110 di 900, prendi 110 dei numeri scritti sopra, fa 71026 moggi di frumento per 347 1010107 bizanti; e 71026 moggi di orzo per 576 1010106 bizanti; e 21012 moggi di miglio per 486 1010102 bizanti; e 21012 moggi di fave per 691 1010102 bizanti; e 21012 moggi di lenticchie per 259 1010101 bizanti. |
x1 + x2 + x3 + x4 + x5 = 90
29 x1 + 25 x2 + 22 x3 + 18 x4 + 16 x5 = 84004 x1 = x2 x3 = x4 = x5 
|
|
Altro sull'acquisto di biade. |
||
|
(XI.7.8 ; G: XI.156)
Ma in verità se tu vuoi ipotizzare che egli abbia avuto quantità differenti di ciascuna delle predette biade; diversamente da quello che dicemmo sopra sulla disuguaglianza di monete, vogliamo dire ciò: se vuoi risolvere problemi simili in tre modi differenti, supponi che abbia comprato quanto vuoi di una di esse. E perché ciò risulti più facile, supponi che abbia comprato 5 moggi di quella che vale 25 bizanti: poiché questi 5 moggi valgono
141 bizanti, sottrai questi 5 moggi da 90, restano 85 moggi; poi sottrai
141 da
1421, restano 20 bizanti. Ora a noi restano da dividere 85 moggi per i 20 bizanti tra le altre quattro biade. Per cui porrai a piacere che di quella che vale 16 bizanti ne abbia comprato 25 moggi, che valgono 4 bizanti; restano 60 moggi per i 16 bizanti da dividere tra le restanti tre biade. Di nuovo supponi a piacere, che abbia comprato 10 moggi di quella biada, che costa 18 bizanti per 100 moggi, questi 10 moggi valgono
451 bizanti: per cui tolti i 10 moggi da 60 e
141 bizanti da 16, restano 50 moggi da dividere per
1514 bizanti tra quella stessa biada, un centinaio della quale vale 22 bizanti, e quella che vale 29 bizanti; perciò bisogna dire: se 56 moggi di due quantità miste di biada valgono
1514 bizanti; quanto valgono 100 moggi. Moltiplicherai allora 100 per
1514, e dividerai per 50, cioè lo raddoppierai, farà
2528 bizanti: dirai quindi: ho moneta da 29, e da 22; e voglio fare da esse 50 libre di moneta da
2528: scritta pertanto la suddetta divisione, come più sopra si è insegnato, prendi la differenza, che c'è da 22 a
2528, cioè
256; e scrivila sopra il 29; e da
2528 a 29 mancano
35, ponilo sopra il 22, e fai la somma di
256 e di
35, fa 7: per questo dividi la moltiplicazione di
356 per 50, farà
2745 moggi, e tanto ha comprato di quella biada da 29 bizanti: e di nuovo dividerai per quel 7 la moltiplicazione di
35 per
(PdA)
50: farà
274 moggi, e tanto ha comprato di quella che vale 22 bizanti.
La costruzione del verbo transitivo multiplico con in + acc. o abl. del moltiplicatore non è l’unica adottata da Leonardo. In alternativa troviamo la costruzione con per + acc. (attestata a partire dal sec. III d.C.). Con il verbo dividere il divisore è generalmente espresso da per + acc. Anche la costruzione con in + acc. non manca tuttavia di qualche sporadico esempio nel Liber abbaci [PdA,pag.9]
|
x2 = 5
x5 = 10 x4 = 25 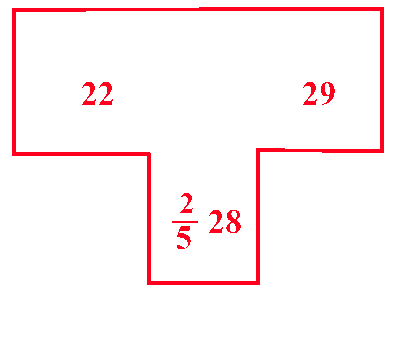
|
|
|
Altro sulle stesse biade. |
||
pg.163 |
(XI.7.9 ; G: XI.161)
E invece uno supponesse di avere comprato di quella da 29 tanto quanto ha comprato, e di quella da 25 la sua quarta parte; di quella da 22 tanto quanto comprò, e di quello da 18 la quarta parte della stessa da 22; di quella da 16 la quinta di quella da 18
[NdT]
Abbiamo coretto il testo per renderlo coerente con il seguito
e così di avere avuto, nelle condizioni prescritte, 90 moggi di quelle cinque biade per
1421 bizanti; si deve fare così: si scriva il problema come si vede più in basso: visto che di quella da 25 compra la quarta parte di quella da 29, dunque compra tanto di quella da 29, e da 25,
14 di quella. Quindi si deve porre 4 sopra il 29 e 1 sopra il 25; e si deve moltiplicare il 4 per il 29, fa 116; e 1 per il 25, fa 25; sommalo con il 116, fa 141; dividilo per la somma di 4 e 1, cioè per 5, fanno
1528 bizanti; e tanto è il valore di 100 moggi di quelle predette biade così commiste. E ancora nello stesso modo, avendo comprato di quella da 22 quanto ha comprato; e di quella da 18 la quarta parte di essa; e di quella da 16 la quinta parte di quella da 18; si chiede in quale numero siano contenuti
1514: per l'appunto nel 20, che dovrai scrivere sopra il 22; e prendi la quarta parte di esso, che è 5; e scrivilo sopra il 18; e ancora prendi
15 di esso, che è 1, e ponilo sopra il 16: e moltiplica 20 per 22, fa 440; e 5 per 18, fa 90; e 1 per 16, farà 16; sommalo con 90 e con 440, fa 546; dividilo per la somma di 20 con 5 e con 1, cioè per 26, fa 21; e tanto è il valore di 100 moggi delle tre biade restanti mescolate assieme nella detta proporzione. Per riportare questo problema alla lega di monete dirai: ho moneta da
1528 e da 21, e voglio di lì fare 90 libre di moneta da
15
2923 once.
|
x2 =
14 x1
x4 = 14 x3 x5 = 15 x4 |
| (XI.7.10 ; G: XI.164) Se desideri fare magistralmente e con arte questa operazione di messa in lega, scritti i dati, moltiplica il 28 per 5 e somma 1; fa 141, moltiplicalo per 9 e per 2 che sono sotto la frazione del 23: fa 2538, ponilo sopra il 28. Poi moltiplica il 21 per 9 e per 2 che sono sotto la frazione del 23 e per il 5 della frazione del 28, fa 1890 che devi scrivere sopra il 21. Ugualmente moltiplica il 23 per il 9 e somma il 5, poi moltiplica per il 2 e somma l'1, fa 425, poi moltiplica per il 5 che sta sotto la frazione che è con il 28, farà 2125 che devi scrivere sopra 15 2923; e di nuovo dirai: ho moneta da 2538 e da 1890; e voglio ricavarne 90 libre da 2125 once: per cui la differenza, che c'è da 1890 fino a 2125, cioè 235, è da porre sopra 1528; e la differenza che c'è da 2125 fino a 2538, cioè 413, è da porre sopra il 21, come è più in basso. |
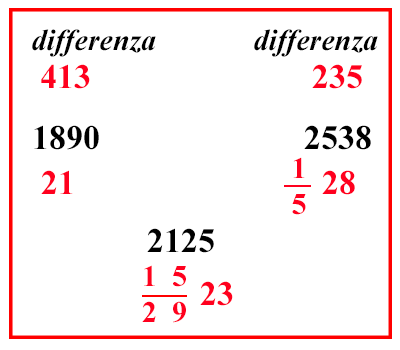
|
|
| pg.164 | (XI.7.11 ; G: XI.166) Somma pertanto 413 con 235, fa 648; per la cui regola, che è 100 899, deve essere divisa la moltiplicazione dei 90 moggi detti sopra per 235, e il totale che ne verrà sarà la somma di quei due moggi di grano sommati più sopra, cioè di 29 e di 25: ma affinché la parte dell'uno sia divisa dall'altra, moltiplica il prodotto della prescritta moltiplicazione, cioè di 235 per 90, per il 4 che sta sopra il 29 nel riquadro; e dividi per la somma di quel 4 con l'1 che è posto sopra il 25, cioè per 5, e per la prescritta frazione, cioè per 1000 49910. E poiché si vede in modo molto evidente che la regola del 90 è nella prescritta frazione. cioè 10 910, non occorre moltiplicare 235 per 90; ma risparmia la fatica della moltiplicazione, e la fatica della divisione per tale 90, e resterà soltanto 235 da moltiplicare per 4 , e da dividere per 10 49: anche di questi, semplificando 14, resterà 235 da dividere per 9, fa 1926 moggi, e tanto comprò di quella da 29. Ugualmente con lo stesso metodo e ordine moltiplica 235 per l'1, che sta sopra il 25, fa 235; dividilo similmente per 10 49, fa 34 496; e tanto compra di quella da 25. E ancora per calcolare le quantità delle restanti tre biade sommate assieme, si dovrebbe moltiplicare 413 per i 90 moggi, e dividere per 100 899: ma per separarle l'una dall'altra, si deve moltiplicare quella moltiplicazione, cioè 413 per 90, per il 20 che è posto sopra il 22; e dividere per la stessa regola cioè per 100 899, e per 26, che è la somma di quel 20 e del 5, che sta sopra il 18, e dell'1, che sta sopra il 16, disposti tutti nel modo migliore nella frazione così: 10000 289913; e così si avrà la quantità di quello che ha comprato in ragione del 22: ma poiché di nuovo si vede in modo assai evidente che 19 del suddetto 90 è sotto la frazione della divisione, prendi 19 di 90, che è 10; e moltiplicalo per 413, fa 4130; moltiplicalo ancora per la metà di 20, così puoi tralasciare 12, che è nella frazione, fa 41300: dividila solo per 100 8913, sono 451 891344 moggi e tanto compra della biada da 22. Ugualmente per sapere quanta ne compra di quella da 18, moltiplica 413 per 5, cioè per la diciottesima parte di 90; poiché è possibile togliere dalla detta divisione, cioè da 10000 289913, la regola del 18, che è 10 29; sottratta questa dalla frazione, resterà da dividere solo per 100 8913 la moltiplicazione di 413 per 5, e ancora per l'altro 5, che è posto sopra il 18; il risultato di tutta questa moltiplicazione è 10325: dividilo per 100 8913, farà 530 891311 moggi; e tanto compra di biada da 18. Ugualmente per avere la quantità che compra del grano da 16: moltiplica 413 per 5, cioè per un diciottesimo di 90, farà 2065; moltiplicalo per l'1 che è sopra il 16, fa ugualmente 2065; dividilo per 100 8913, farà 162 89132 moggi; e tanto ne compra della biada da 16, come si mostra nel riquadro. |

|
Della campana di 5 metalli.
|
||
| (XI.7.12 ; G: XI.172) Un tale voleva fare una campana di cinque metalli, tra questi un cantare di uno vale 16 lire; di un altro invero 18 lire; e di un altro 20 lire; di un altro ancora 27 lire; di un altro poi 31 lire: e così fece con essi una campana, pesante 775 rotoli, che pagò 34162 lire: si chiede quanto mise di ciascun metallo: tutto questo lo puoi fare con il sistema usato per le biade. Ma perché si capisca più chiaramente, vediamolo con i rotoli:775 rotoli di metalli misti, valgono 34162 lire, quanto valgono 100 rotoli, cioè un cantare; devi fare così così: moltiplica 34162 libre per 100, fa 16275; dividilo per la regola di 775, che è 100 5531; fa 21. Poi per riportare questo problema alla messa in lega delle monete, dì così: ho moneta da 31, da 27, da 20, da 18, e da 16; e voglio farne 775 libbre di moneta da 21 lire: In questa fusione, se non hai dimenticato tutte le dimostrazioni simili, troverai che ha messo nella suddetta campana, 29 311187 rotoli del metallo da 16 per 30 lire e 61114 denari; e del metallo da 18 29 311187 rotoli per 33 lire e 16 soldi e 4114 denari, e del metallo da 20 29 311187 rotoli per 37 lire e 2 soldi e 2116 denari; e del metallo da 27, 17 211105 rotoli per 28 lire e 10 soldi e 2118 denari, e del metallo da 31, 17 211105 rotoli per 32 lire, e 15 soldi, e 8112 denari. E se nella suddetta campana vorrai mettere quantità disuguali di ciascun metallo, farai secondo ciò che abbiamo spiegato prima per l'acquisto di 90 moggi di 5 biade; e se vuoi avere tutti i valori in rotoli interi, lavora con il sistema delle leghe; e avrai del metallo meno caro 60 rotoli, del successivo 155 rotoli , del terzo 400, del più caro 40; e anche questi valori possono essere calcolati diversamente, col sistema delle leghe, in diversi numeri interi: per cui il prezzo del primo metallo sarà di 9 lire e 12 soldi; del secondo 27 lire, del terzo 80 lire; del quarto 33 lire, e 15 soldi; del più caro 12 lire, e 8 soldi. |

|
|
Un uomo compra 30 uccelli di tre tipi per 30 denari.
|
||
pg.165  matematica delle leghe |
(XI.7.13 ; G: XI.176) Un tale comprò 30 uccelli per 30 denari. Tra questi ci furono pernici, colombe, e passeri: le pernici le comprò per 3 denari; la colombe per 2 denari, e 2 passeri per 1 denaro, cioè 1 passero per 12 denaro. Si chiede quanti uccelli comprò di ciascun tipo: dividi i 30 denari per i 30 uccelli, farà 1 denaro. Dì allora: ho moneta da 12, e da 2, e da 3; e voglio farne moneta da 1. In problemi simili si deve procedere nel modo delle leghe, per avere numeri interi di uccelli. Perciò, per equiparare le specie degli uccelli meno cari con quelle degli uccelli più cari, dirai: ho moneta da 12, e da 12, e da 2, e da 3; e voglio farne moneta da 1, cioè ho moneta da 1, e da 1, e da 4, e da 6; e voglio farne moneta da 2: fa la prima unione di passeri e pernici; e saranno 5 uccelli per 5 denari, cioè 4 passeri e 1 pernice, e fai una seconda unione di passeri e colombe, e avrai 3 uccelli per 3 denari, cioè 2 passeri e 1 colomba: poi, per avere 30 uccelli mischiati tra loro, metti la prima unione tre volte, per cui ci saranno 12 passeri, e 3 pernici; e rimarranno 15 uccelli da unire; per questi metti la seconda unione 5 volte, e avrai 10 passeri e 5 colombe; e così tra gli uccelli suddetti ci saranno 22 passeri, e 5 colombe, e 3 pernici, come si mostra nel riquadro. E sappi che degli uccelli scritti sopra potrai averne un qualunque numero intero per quanti ne vorrai per altrettanti denari oltre i 15, ma sotto i 15 non si possono avere uccelli, se non in numero di 13 e 11 e 8: a 13 uccelli va a finire la prima lega due volte, e la seconda 1 volta; e negli 11 uccelli va a finire la seconda lega due volte, e la prima una volta sola, e in 8 uccelli va finire una volta ogni fusione. |
x1 + x2 + x3 = 30
6 x1 + 4 x2 + x3 =
2 (x1 + x2 + x3)
(1, 0 , 4) è una soluzione
(0, 1 , 2) è una soluzione
a (1, 0 , 4) + b (0, 1 , 2)
è la soluzione genarale. 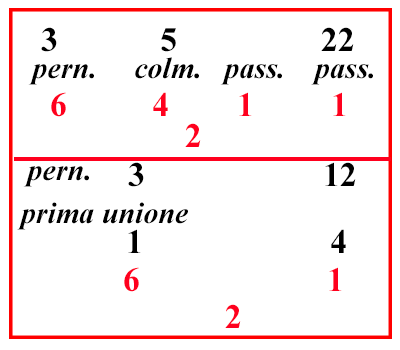
|
Sullo stesso.
|
||
| (XI.7.14 ; G: XI.180) E ancora la pernice valga 2 denari, 2 colombe siano date per 1 denaro; e 4 passeri per 1 denaro; e voglio 12 uccelli per 12 denari: quindi hai moneta da 14, e da 12, e da 2; e vuoi farne moneta da 1: fa una prima unione di pernici e passeri; e saranno 7 uccelli per 7 denari, cioè 4 passeri, e 3 pernici: e fai una seconda unione di pernici e colombe; e saranno 3 uccelli per 3 denari, cioè 2 colombe e 1 pernice. Ma poiché con queste due unioni non possiamo mettere insieme 12 uccelli con numeri interi per 12 denari, uniamo a loro 24 uccelli, cioè il doppio dei 12 uccelli, nei quali va a finire per tre volte la prima unione, e una volta la seconda. Perciò di questi 24 uccelli, 10 saranno pernici, e 2 colombe, e 12 passeri: i quali numeri, essendo pari, si possono dividere esattamente a metà. Perciò dimezzali e avrai 5 pernici, 1 colomba, e 6 passeri, e cioè 12 uccelli per 12 denari. E se si supporrà che una colomba valga solo 1 denaro, allora avrai bisogno solo della prima unione, nella quale ci sono 3 pernici, e 4 passeri per 7 denari. I 5 uccelli che restano saranno colombe: se poi da questi vuoi fare una unione di 100 uccelli per 100 denari, puoi impiegare la prima unione quante volte vorrai, finché il 100 superi il totale dell'unione; e ciò che resterà dal 100 saranno colombe. | ||
Sullo stesso argomento quando i tipi di uccelli sono quattro.
|
||
|
soluzione (XI.7.15) 100uccelli.py |
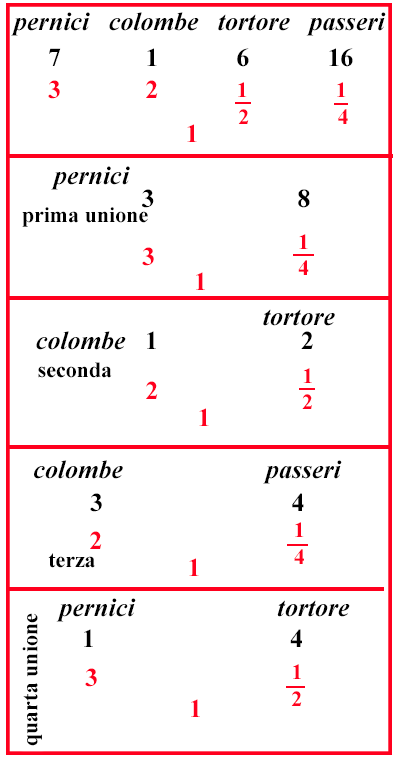
(XI.7.15 ; G: XI.183) Ugualmente una pernice vale 3 denari, una colomba 2, una tortora 12 denaro, un passero 14 di denaro; e vuoi 30 uccelli di questi per 30 denari: fai una prima unione di pernici, e passeri; e hai 11 uccelli, cioè 3 pernici, e 8 passeri: e in una seconda unione ci saranno 2 tortore, e 1 colomba, cioè 3 uccelli. Ma con queste due unioni non si possono mettere insieme 30 uccelli; visto che sottratta da 30 la prima unione usata una volta e due, non resta un numero divisibile per 3, cioè per il totale della seconda unione. Perciò bisogna cambiare le unioni: fai perciò una terza unione di colombe, e passeri e avrai 7 uccelli, cioè 3 colombe e 4 passeri: restano per la quarta fusione 5 uccelli, cioè 4 tortore e 1 pernice: quindi in tutti i problemi simili devi considerare una prima unione, e una seconda, o una terza, e una quarta qualche volta; e allora ingegnati a completare il totale cercato, a seconda di quanto risulterà da una o più di esse. Per esempio: poniamo che il totale della prima, e della seconda unione una volta, siano 14 uccelli, sottratti questi da 30, restano 16 uccelli da aggiungere all'unione, per i quali rientra una volta la prima unione, e la quarta, oppure tre volte la seconda, e una volta la terza: quindi in questi 30 uccelli rientra due volte la prima unione due volte la seconda, e una volta la quarta; e così avrai 7 pernici, e 1 colomba, e 6 tortore, e 16 passeri. Oppure mettiamo in questi 30 uccelli la terza e la quarta unione; e saranno 12 uccelli, sottratti i quali da 30, resteranno 18 uccelli, nei quali rientra una volta la prima unione e la terza, o tre volte la quarta unione, e una volta la seconda; così avrai 4 pernici, 6 colombe, 4 tortore, 16 passeri: e così possono unirsi in diversi modi; quando le specie siano 4 o anche di più. E nota, che quando di una qualche specie di uccello sia posto 1 uccello per 1 denaro, allora il problema è facilissimo; poiché tralasci quella specie; fai le unioni delle altre, e completa il totale richiesto aggiungendo la specie tralasciata. |
x1 + x2 + x3 + x4 = 30
3 x1 + 2 x2 +12 x3 +14 x4 =
(x1 + x2 + x3 + x4)
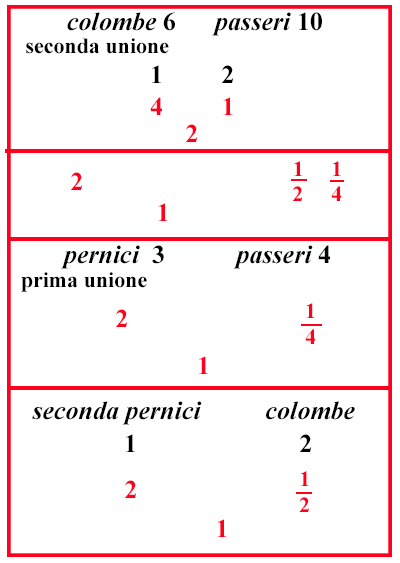
|
Termina l'undicesimo capitolo.
|
|
|