
Quarta Differenza.
|
||
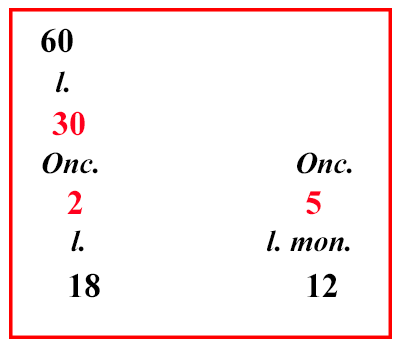
| (XI.4.1 ; G: XI.44) Se avessi una moneta da 5 once, dalla quale volessi fare 30 libbre di moneta da 2 once solamente aggiungendo rame rosso, e volessi sapere quanto argento metterai della moneta stessa, e quanto di rame rosso, calcolerai quanto argento deve esserci in quelle 30 libbre della moneta da fare: ovviamente 60 once: poiché in ogni libbra ci devono essere 2 once d'argento, e due volte 30 fa 60; queste 60 once d'argento sono in 12 libbre di quella moneta da 5 once che hai; poiché la divisione di 60 per 5 fa 12; e tante libbre metterai della suddetta moneta. Quanto manca poi per arrivare a 30 libbre, cioè 18, lo metterai di rame rosso. |
|
|
Sullo stesso.
|
||
| pg.149 |
(XI.4.2 ; G: XI.45)
E se avessi due monete di maggior valore rispetto alla moneta che vuoi fare, delle quali una sia da 7 once, e l'altra da 6 once, con le quali vuoi fare una libbra di moneta, in cui ci siano 4 once d'argento; e volessi sapere quante once di ciascuna metteresti, e anche l'aggiunta di rame. La lega può essere realizzata in tre modi diversi secondo tre sequenze diverse. Il primo prevede senz'altro che si metta la medesima quantità da ciascuna delle monete indicate. Il secondo che vengano considerate quantità diverse. Il terzo in modo proporzionale. Per cui se nella lega scritta sopra, vuoi mettere in modo uguale; da ciascuna delle monete indicate aggiungerai le once d'argento, che sono in entrambe le monete, cioè 7 con 6, farà 13; e moltiplica l'argento di quella moneta che vuoi per le 12 once, cioè per una libbra che vuoi fare in lega, saranno 48 once; dividile per le dette 13, farà
9133 once, e tanto metterai di ciascuna moneta. Quanto manca poi per arrivare fino a 12 once, cioè alla libbra, lo metterai in rame
[NdT]
ndt: qui per la parola rame è utilizzata proprio la parola "rame" in luogo del latino classico "es, eris" o "cuprum"
, cioè
8134 once.
|
x1 libbre da 7 once
fanno x1 × 712 once d'argento  |
Sullo stesso mettendo in modo diseguale da ciascuna moneta.
|
||
(XI.4.3 ; G: XI.47) E se vuoi mettere in misura disuguale [NdT]
"uguale" nel testo è un chiaro errore
da ciascuna moneta nella moneta in lega descritta precedentemente, supponi di avere una libbra di quella moneta, che è da 6 once, e 2 libbre dell'altra [ da 7 once ]; e scriverai nel riquadro l'1 sopra il 6 e il 2 sopra il 7, secondo il modo della seconda differenza; e moltiplicherai l'1 per il 6, farà 6; e il 2 e il 7, farà 14; e porrai il 6 sopra l'1, e il 14 sopra il 2; e sommali insieme, farà 20: poi moltiplica il 4 per il 12, cioè le once d'argento che vuoi porre in una libbra, per l'oncia che vuoi fare in lega, farà 48; moltiplicalo per l'1 che è scritto sopra il 6, farà 48; dividilo per il 20 scritto sopra, farà
252 once e tanto metterai di quella moneta che è da 6 once. Ugualmente moltiplica 48 per il 2 che sta sopra il 7, e dividi per 20, farà
454 once; e tanto metterai di quella che è da 7 once: a cui aggiungerai le
252 once scritte sopra, farà
157 once, alle quali per arrivare alle 12 once, cioè fino alla libbra che vuoi fare in lega, mancano
454 once che aggiungerai [ dal rame ].
|
6 x1 + 7 x2 = 48
x2 = 2 x1  |
|
| (XI.4.4 ; G: XI.49) E se vuoi fare una lega rispettando una proporzione, cioè così come un certo numero dato sta ad un altro numero dato, così ciò che metterai di una moneta sta a ciò che metterai dell'altra: e così diciamo: come 3 sta a 4, così ciò che metterai della moneta, che è da 6 once, sta a ciò che metterai della moneta che è da 7 once, e poniamo che vuoi di lì fare in lega 23 libbre da 5 once. Poni quindi il 3 sopra il 6, e il 4 sopra il 7, che sono i numeri della proporzione data; e moltiplicherai 3 per 6, farà 18; e 4 per 7, farà 28; porrai il 18 sopra il 3, e il 28 sopra il 4; e li sommerai insieme, farà 46: e moltiplica 5 per 23, farà 115; moltiplicalo per il 3 che è sopra il 6, e dividilo per 46, faranno 127 libbre di moneta da 6 once: similmente moltiplica 115 per 4, e dividi per 46, faranno 10 libbre di moneta da 7 once; sottratte queste 127 libbre, e queste 10 libbre, cioè 1217 libbre, dal totale della lega, cioè dalle 23 libbre, restano 125 libbre per l'aggiunta di rame. |
x1 : x2 = 3 : 4 6 x1 + 7 x2 = 115 x1 = 3 x x2 = 4 x |
|
Su tre monete quando si mettano parti uguali di ciascuna.
|
||
| (XI.4.5 ; G: XI.51) E se avessi tre monete, delle quali una è da 123 once, una da 134 once, un'altra da 345 once, e volessi mettere parti uguali di ciascuna moneta e fare in lega 10 libbre da 152 once, somma l'argento che è in ciascuna moneta, farà 71213 once; e moltiplica l'argento di quella stessa moneta che vuoi fare, cioè 152 once per le 10 libbre, farà 22, dividilo per 71213 libbre, farà 1011631 once; e tanto metterai di ciascuna moneta. Il resto poi che c'è per arrivare a 10 libbre, che è 231635 libbre, lo metterai di rame rosso. |
72 x1 +
133 x2 +
234 x3 = 22
x1 = x2 = x3 
|
|
Sullo stesso quando si metta in modo disuguale o proporzionale di ciascuna moneta.
|
||
pg.150 |
(XI.4.6 ; G: XI.52) Dunque se vuoi impiegare quantità diverse, e proporzionali di ciascuna moneta, in modo da dire: come 2 [non è scritto nel testo] sta a 3, così ciò che metterai della moneta che è da 123 once sta a ciò che metterai della moneta che è da 134 once; e come 4 sta a 5, così ciò che metterai di quella da 134, sta a ciò che metterai di quella da 345. Troverai pertanto tre numeri, il primo dei quali sta al secondo come 2 a 3; e il secondo al terzo come 4 a 5; il modo di trovarli è porre su una linea il 2 e il 3: scrivi il 4 sopra il 3; e dopo il 3 poni il 5; e moltiplica il 4 per il 2 che gli è di traverso, farà 8 per il primo numero; e moltiplica il 4 per 3, farà 12 come secondo numero; e il 3 per il 5 che gli si oppone in diagonale, farà 15 come terzo numero. O altrimenti poiché 2 di 3, sarà 23, e 4 di 5 sono 4/5, guarda in quale numero si trovino 4523, cioè in 15, di cui calcoliamo i 45, cioè 12, di cui come secondo numero, calcoliamo i 23, cioè 8, che consideriamo come primo numero. Infatti l'8 sta al 12 come il 2 sta al 3 e il 12 sta al 15 come il 4 sta al 5: poi porrai l'8 sopra 123, e il 12 sopra 134 e il 15 sopra 345, come si mostra nel riquadro: e vedi se il rotto che è in ciascuna moneta, si trovi nel numero posto [ in corrispondenza ] sopra. Infatti 12 si trova nell'8, e 13 nel 12, ma 14 non si trova nel 15, né in alcuna parte di esso. Dunque affinché tu abbia il meglio di ciò che vuoi, è necessario che si moltiplichino ciascuno dei numeri posti sopra per 4, farà 32, e 48, e 60; e moltiplicherai 123 per 32, farà 112, che devi scrivere sopra il 32. E 134 per 48, farà 208, ponilo sopra il 48; poi 5 per 60, farà 345 ponilo sopra il 60, e sommerai 112 con il 208, e con 345, farà 665. E moltiplica le 10 libbre che vuoi fare in lega, per le 152 once, farà 22, moltiplicalo per 32, e dividerai per 665, farà 401 57191 libbre di moneta, che è da 123. Ugualmente moltiplicherai il 22 per 48 e dividerai per 665: farà da quella, che è da 134, 1111 57191. Ugualmente moltiplicherai lo stesso 22 per 60 e dividerai per 665, si considererà di quella moneta che è da 345, 518 7191 libbra. E il resto poi lo metterai di rame rosso, che è 007 57195 libbre, resto che si trova allo stesso modo in cui si calcola la parte di profitto dell'ultimo socio con le parti già trovate degli altri. Dunque dalle frazioni scritte sopra potrai fare le once e le parti di once secondo ciò che abbiamo mostrato nelle transazioni commerciali. |
72 x1 +
133 x2 +
234 x3 = 22
x1 : x2 = 2 : 3 x2 : x3 = 4 : 5 
x1 = 8 x x2 = 12 x x3 = 15 x 
|
Termina la quarta differenza dell'undicesimo capitolo.
|
|
|