I VIAGGI

Piccola premessa

La classe a cui è stata proposta l’attività relativa ai problemi sui viaggi è una quarta liceo scientifico opzione scienze applicate. È una classe molto eterogenea, composta da 18 studenti con due studenti con DSA lieve. La classe ha risentito molto dei problemi portati dalla pandemia, avendo passato oltre agli ultimi tre mesi del secondo anno in DaD, gran parte del terzo anno.Inoltre, più in generale, ha risentito dei problemi portati dalla discontinuità didattica, anche negli anni precedenti, indipendentemente dalla pandemia. Nel biennio la geometria euclidea è stata trattata pochissimo, per cui gli studenti presentano notevoli difficoltà nel ragionamento geometrico, e la risoluzione di problemi di qualsiasi genere ha avuto un ruolo molto marginale. Per questi motivi un buon gruppo di alunni presenta lacune notevoli, e la maggior parte della classe lavora con difficoltà sullarisoluzione di problemi e, più in generale, presenta difficoltà nella lettura, nell’analisi e nell’interpretazione di testi, come concordano anche i colleghi delle altre discipline.

Queste attività sono pensate per far lavorare gli studenti in gruppo, aiutandoli a recuperare quella socialità, quello scambio e quella condivisione che in DaD sono mancate. Questo consente di coinvolgere anche gli studenti meno attivi.

La classe possiede le conoscenze di base sulle funzioni. Le attività proposte hanno come scopo quello di applicare quanto noto sulle funzioni alla risoluzione di alcuni problemi, partendo però da un approccio intuitivo, per consentire anche agli studenti più deboli di affrontare il lavoro. Essendo questo un indirizzo in cui non si studia il latino, gli studenti hanno avuto il testo tradotto a disposizione.

Prima di iniziare a lavorare sul testo ho fatto una piccola premessa sul “Liber abaci” e sull’importanza che esso storicamente riveste. Gli studenti sono rimasti molto stupiti dal fatto che, prima di allora, in Europa non si potesse operare con i numeri razionali, e che il concetto di equazione non esistesse. Probabilmente nella loro mente la matematica è un ente astratto che è sempre esistito. Personalmente credo che questa concezione derivi dall’idea che la matematica non è il frutto di un lavoro intellettuale di uomini come noi, ma consiste in qualcosa di preesistente e quasi inaccessibile ai più. In ogni caso va detto che gli studenti si sono messi volentieri alla prova, prendendo le attività proposte quasi come fossero degli enigmi da risolvere.

L’attività 1 e gran parte dell’attività 2 sono state più complesse per gli studenti, in quanto si chiedeva di “scoprire” qualcosa, nell’ultima parte dell’attività 2 e nell’attività 3 si chiedeva l’applicazione di quanto scoperto precedentemente, cosa che ha creato certamente meno difficoltà a livello di ragionamento, ma più difficoltà nella formalizzazione, altro tallone d’Achille.

Relazione sull’attività 1

Risoluzione intuitiva del problema proposta da Fibonacci

Lo svolgimento dell’attività ha richiesto 1 ora.

Gli studenti sono stati divisi in piccoli gruppi. Come prima attività ho proposto il problema così come presentato nel “Liber abaci”, chiedendo agli studenti di risolverlo con qualunque metodo avessero ritenutoadatto allo scopo, questo per stimolare anche gli alunni con più difficoltà ad impegnarsi, non essendo richiesta nessuna conoscenza particolare.Ho chiesto, inoltre, di provare a trovare due modi diversi di trovare la soluzione. Unica richiesta inderogabile: il ragionamento deve essere esposto, non necessariamente in una forma matematica, ma comunque in modo chiaro, per iscritto.

Questo approccio ha funzionato, ogni gruppo, con i propri mezzi, ha risolto il problema, alcuni gruppi hanno ricavato autonomamente, seppure, in alcuni casi con una formalizzazione rozza, sia la regola diretta che la regola inversa.

Approccio con regola diretta

Qui osserviamo la risoluzione di un’equazione in cui è stato posto f ( f  f ( x  ) ) = 0, dove f ( x ) = 2 x − 12 calcola il denaro in possesso del mercante dopo un viaggio, avendo x come capitale di partenza.

Approccio con regola inversa

In questo caso lo studente ha dimostrato, esponendolo con estrema semplicità e chiarezza, di aver compreso cosa significa invertire una funzione.

Anche se in modo piuttosto rozzo e, praticamente, senza alcuna formalizzazione, questo ragionamento, proposto in modo praticamente identico da due gruppi diversi, consente di determinare i denari posseduti dal mercante, sapendo che alla fine sarà rimasto senza nulla.

Un altro approccio

I precedenti non sono stati gli unici due approcci, qualcuno ha proposto una risoluzione per tentativi, da cui è scaturito anche un abbozzo di metodo iterativo, una sorta di “metodo di bisezione”, utilizzato però con una certa inconsapevolezza. Potrebbe essere uno spunto interessante per lavorare sulla risoluzione di equazioni utilizzando metodi iterativi.

Una piccola osservazione: del gruppo che ha proposto la risoluzione “per tentativi” facevano parte i due studenti con DSA, uno dei quali è stato il promotore di questo metodo. Utilizzando inconsapevolmente la continuità della funzione e il teorema di esistenza degli zeri, hanno in effetti determinato la soluzione del problema.

L’idea di procedere per tentativi si ritrova in Fibonacci con la “falsa posizione”e con la “doppia falsa posizione” trattata diffusamente nel capitolo XIII del Liber abaci. A livello matematico è probabilmente un’idea superata, ma credo che possa avere una valenza didattica, soprattutto quando si cerca di coinvolgere gli studenti con difficoltà perché ciò consente loro di superare quel blocco che sempre più spesso mi trovo a riscontrare, e cioè l’idea del “Non so farlo, non sono capace”. Se lo studente può procedere per tentativi, in qualche modo, è costretto a provare una risoluzione. In sostanza, stiamo eliminando l’alibi che si crea.

Variazioni sul tema

Un gruppo mi ha chiesto di poter proporre una variazione sul testo del problema. Ho accolto la richiesta e qui riporto quanto mi hanno consegnato.

La risoluzione del problema sembra non essere coerente con il testo proposto, che peraltro è ambiguo.

Probabilmente gli studenti non hanno saputo tradurre in un linguaggio formalmente corretto l’idea che avevano in mente, e che mi hanno esposto oralmente. Ciò è coerente con il profilo della classe in questione, che risulta piuttosto carente anche nelle competenze relative alla lingua italiana.

Al di là dell’intento evidentemente ludico, e della risoluzione non corretta del problema, ho trovato interessante il fatto che gli alunni si siano sentiti stimolati ad inventare situazioni nuove, a creare problemi da risolvere, attività che di rado si fa in classe e che, forse, meriterebbe più attenzione.

Alcune osservazioni

Agli studenti non è stata fornita la soluzione numerica del problema, in questo modo sono stati costretti a verificare la bontà del loro lavoro, cosa che autonomamente non fanno mai. È chiaro che i libri di testo riportano le soluzioni dei quesiti per favorire l’autocorrezione, ma in questo modo gli studenti sono portati a non chiedersi mai se la soluzione trovata è corretta e, quando non ce l’hanno a disposizione, capita anche che vadano nel panico (situazioni vissute durante le verifiche, in cui non fornisco mai la soluzione dell’esercizio).

Un fatto curioso che ho osservato: mentre per quanto riguarda la regola diretta i ragazzi hanno dato autonomamente una forma matematica al loro ragionamento (un’equazione o, addirittura, alcuni già in prima battuta hanno utilizzato la composizione di funzioni per poi ottenere un’equazione da risolvere), per la regola inversa nessuno dei gruppi lo ha fatto autonomamente. Probabilmente il primo metodo rientra in quelle procedure quasi standardizzate in cui spesso, nella scuola, si rischia di cadere.

Questa attività è stata più articolata e ha richiesto due ore. Anche questaattività è stata svolta in gruppi, mantenendo la prima suddivisione fatta.

Il mio compito è stato quello di girare tra i vari gruppi, discutendo con gli studenti le loro strategie e spingendoli ad argomentare e a discutere, proprio quel processo che è alla base della scoperta e della conoscenza.

Prima parte: caccia all’errore

Nella prima parte ho chiesto ai ragazzi di commentare la risoluzione sbagliata del problema, che ho preso da una scheda inviatami dal prof. Ghione:

Riporto alcuni commenti dei ragazzi:

I ragazzi hanno avuto difficoltà con questa richiesta, più che altro perché hanno avuto difficoltà a spiegare con le parole ciò che in qualche modo avevano intuito, e cioè che i 12 denari vanno sottratti di volta in volta, in quanto nel viaggio successivo si raddoppiano i denari in possesso del mercante, considerata anche la spesa.

Questa è stata un’attività molto interessante, dovendo dare conto di un errore commesso da un’altra persona, di fatto, gli studenti sono stati costretti a tentare di argomentare in maniera esauriente il loro ragionamento. In questo momento mi sono resa conto, toccando con mano, di quanto poco questa cosa venga richiesta ai ragazzi nel corso di tutti gli anni che passano a scuola.

Seconda parte: la risoluzione di Fibonacci

Nella seconda parte ho proposto la regola diretta, utilizzando il testo di Fibonacci (tradotto). Ho chiesto agli studenti di provare ad applicare il metodo e di vedere se il metodo risolutivo individuato da loro la volta precedente presentasse delle analogie con quello proposto.

Gli studenti hanno faticato abbastanza a decodificare questa serie di calcoli, alcuni hanno provato a scrivere il procedimento in una forma più moderna.

Anche in questo caso, confrontandomi oralmente con gli studenti ho capito che la maggior parte di loro aveva intuito delle analogie tra il metodo proposto da Fibonacci e i metodi proposti da loro. Come al solito, la difficoltà sta nell’argomentazione.

Terza parte: componiamo le funzioni

Nella terza parte ho richiesto una formalizzazione della regola diretta, utilizzando la composizione di funzioni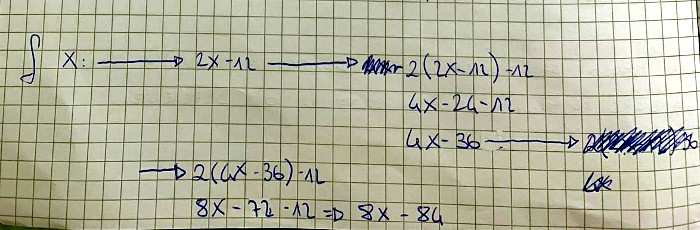

Ho chiesto inoltre di utilizzare la regola diretta per risolvere i problemi ulteriori proposti da Fibonacci (il caso in cui restano 9 denari e quello in cui ne guadagna 9)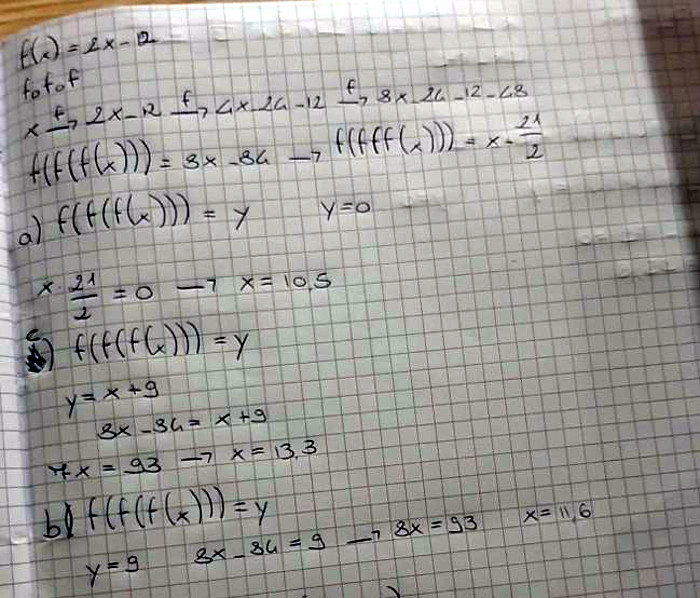

Anche qui si possono rilevare delle difficoltà nella formalizzazione, in particolare nell’uso del segno di uguaglianza, spesso utilizzato in maniera un po’ troppo disinvolta. Ciò lascia trasparire una mancata acquisizione del significato profondo che questo simbolo riveste nel linguaggio matematico.

A questo punto i ragazzi hanno dovuto formalizzare la regola utilizzando un generico fattore a, che indicava l’incremento del capitale per ogni viaggio, s la generica spesa, n il numero di viaggi:

Non tutti gli studenti sono riusciti a generalizzare la regola nel caso di n viaggi, che richiede un buon livello di astrazione e di formalismo matematico.

Quarta parte: un problema diverso

Infine, ho chiesto la risoluzione del problema con quattro viaggi diversi, con l’utilizzo della regola diretta

A questo punto non ci sono state difficoltà, è stato un semplice esercizio. L’unica difficoltà che permane è la decodifica del testo scritto, per cui ho dovuto aiutare pressoché tutti i gruppi a capire cosa il problema stesse chiedendo.

Relazione sull’attività 3

In questa attività, che ha richiesto 1 ora, ho proposto un esercizio simile a quello fatto per la regola diretta, cioè di formalizzare con una funzione la regola inversa e, successivamente, di comporre la funzione trovata con la regola diretta e quella trovata con la regola inversa, verificando che le due funzioni sono inverse.

In realtà lo studente voleva affermare che la funzione F(x) utilizzata per risolvere il problema con la regola diretta è l’inversa di G(x), utilizzata per risolvere il problema ragionando a ritroso. Con il termine “uguali”, utilizzato impropriamente, voleva forse intendere che entrambe risolvono il problema, pur essendo funzioni diverse

Considerazioni finali

Il vantaggio di attività di questo tipo è certamente il fatto che mettono lo studente davanti alla necessità di attingere alle proprie conoscenze, di manipolare la matematica, di partire da un ragionamento concreto e, in alcuni casi, espresso in modo piuttosto “rozzo” e di renderlo astratto, matematico. Questo aiuta certamente a sviluppare le competenze matematiche di cui si parla molto e di cui si dice che andrebbero potenziate. Nella pratica quotidiana non è sempre semplice lavorare in questo modo, però ritengoche l’inserimento di attività di questo tipo, ispirate ai problemi del “Liber abaci” possa portare un grande giovamento nell’apprendimento, essenzialmente per due motivi:

1. I problemi proposti sono spesso risolvibili in modo intuitivo, ciò permette a tutti gli studenti un primo approccio e genera un clima di fiducia, poiché lo studente ha davanti a sé un traguardo raggiungibile;
2. I problemi proposti vengono risolti in più modi, facendo capire allo studente che non esiste LA risoluzione del problema, ma UNA possibile risoluzione del problema, e che la matematica non è un insieme di regole, ma è un insieme di ragionamenti, i quali possono essere tutti validi.

D’altro canto sono attività che richiedono molto tempo e una buona collaborazione da parte dei ragazzi, nonché un notevole sforzo da parte del docente (o dei docenti, laddove si decida di optare per un lavoro pluridisciplinare).

Un’ultima piccola considerazione: qualche tempo dopo gli studenti hanno affrontato una verifica in cui era presente un esercizio sulla composizione di funzioni... la percentuale di studenti che hanno compreso l’argomento e svolto correttamente l’esercizio è stata altissima.