DA PUNTI E NUMERI DI RETTE PER ARRIVARE ALLE PROGRESSIONI ARITMETICHE. Silvia Cerasaro |
|||||
|
Nel capitolo XII del Liber Abaci, Leonardo Pisano Fibonacci affronta diverse tematiche: Interessante quella trattata nel paragrafo XII.1, le progressioni aritmetiche. 
Spesso, per trattare tale argomento, si racconta un aneddoto su Gauss, che risale a quando il matematico aveva 9 anni. Pare che il suo insegnante, per mettere a tacere gli allievi ordinò loro di fare la somma dei numeri da 1 a 100. Quasi subito il bimbo Gauss diede la risposta esatta, sorprendendo l'insegnante. Pare che mise in una riga i numeri da 1 a 100 e in una riga sotto i numeri da 100 a 1, e vide che ogni colonna dava come somma 101: Gauss moltiplicò 100 × 101 e divise per due, ottenendo il risultato. Nel Liber Abaci, invece, viene riportato un metodo molto intuitivo: Fibonacci presenta le progressioni aritmetiche con degli esempi che sfruttano un diagramma a forma di V capovolta o, come dicono i miei alunni, a forma di tetto.
Dalle sue spiegazioni si evince che i termini della progressione da sommare vengono divisi in due metà ed ognuna di esse è posizionata rispettivamente sui lati del diagramma. Nel caso in cui il numero dei termini da sommare sia dispari, il termine centrale sarà posizionato in cima al diagramma. In linguaggio matematico, se si vogliono sommare n termini di una progressione aritmetica a1 + a2 + a3 +....+ an, si possono presentare le seguenti situazioni:
|
|||||
|
Attività didattica: le progressioni e il numero di rette passanti per n punti
Ho conosciuto il contenuto del dodicesimo capitolo del Liber Abaci nel momento in cui nella mia classe prima stavo trattando tematiche in merito ai punti e alle rette nel piano euclideo. Questa classe presenta una situazione particolare, sono 16 alunni, di cui uno con disabilità lieve, 6 con disturbi specifici dell'apprendimento, 6 con bisogni educativi speciali. Viste le difficoltà della maggioranza, ho fissato come mio obiettivo quello di trattare le differenti tematiche puntando sul potenziamento del ragionamento e delle capacità logiche. Lo scopo dell'attività presentata, ovvero dedurre il numero di rette passanti per un numero n di punti non allineati, mira a cercare una strategia che, dal conto concreto, permetta il passaggio all'astratto, mediante una particolare modalità che fa contare in maniera differente. Immaginiamo che Chiara, Valerio, Desirée e Giulia vogliano brindare...quante volte sentiranno il tintinnio dei bicchieri? I miei alunni cominciano a formulare diverse ipotesi, anche discutendo in maniera animata; dalla loro discussione emerge la necessità di disegnare, tanto da capire che gli alunni sono dei punti ed i loro brindisi una retta per passa per essi.
Se siamo solo in due, c'è un unico brindisi perché per 2 punti passa una ed una sola retta. |
|||||
|
Il procedimento ordinato è stato compreso, anche se qualche retta su qualche quaderno non è stata disegnata perché dimenticata. 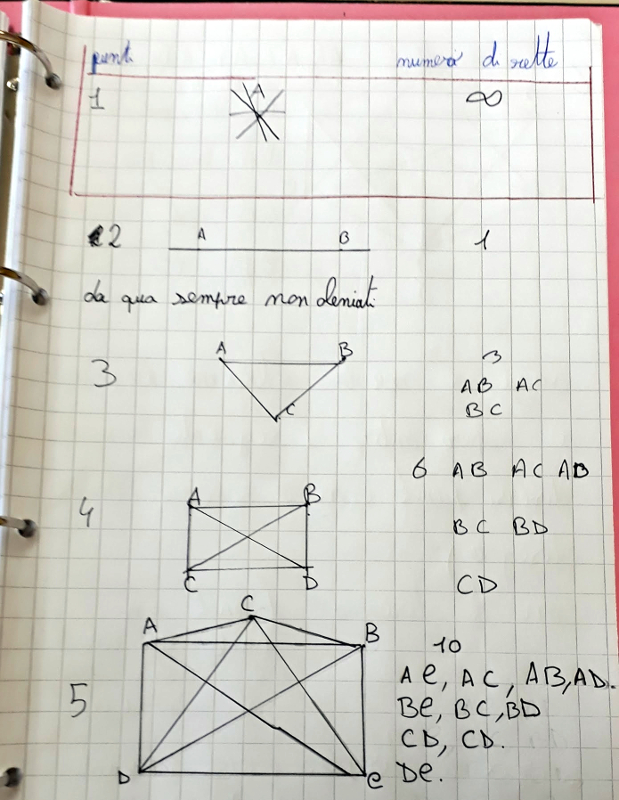
quindi, se per esempio devo contare le rette per 6 punti, faccio 5+4+3+2+1, senza fare il disegno L’intuizione è stata corretta, per contare le rette passanti per n punti si sommano i numeri da 1 a n-1. Gli alunni non sanno che questa somma è una progressione aritmetica e ovviamente non conoscono alcun procedimento per sbrigare questa operazione. |
|||||
|
Assegno, quindi, diversi esercizi tipo i precedenti, ma con un numero maggiore di punti, ad esempio 17. Gli alunni si lamentano per le somme perché ci vuole troppo tempo, fanno le operazioni in ordine di scrittura, quindi svolgono 1+2=3 e lo sommano a 3, ottenendo 6, a cui sommano 4 e così via. In questa situazione presento loro il Liber Abaci, cap.XII e andiamo a leggere il procedimento che Fibonacci spiega per fare le somme sul suo bel diagramma. Desirèe afferma che questo tetto sembra essere d’aiuto, così che si comincia a fare le somme per tutti i casi trattati. 
Il “tetto di Fibonacci” è di grande aiuto per fare queste somme, i ragazzi sembrano aver compreso il suo funzionamento. |
|||||

Assegno come compito a casa di verbalizzare quanto hanno compreso sino ad ora. I ragazzi usano video e relazioni, alcuni preferiscono raccontare oralmente come si fa. 

|
|||||
|
Si passa, ora, a svolgere altre tipologie di esercizio, sfruttando sempre il tetto di Fibonacci. Si vogliono sommare i termini di una progressione formata dai soli numeri pari che vanno da 6 a 18. Come si procede? Le facce degli alunni non sono molto perplesse… i numeri che intervengono sono 6, 8, 10,12, 14,16,18, e sono 7, provo a metterli sul tetto. |
|||||
|
6+18 fa 24, come anche 8+16… non cambia nulla, si svolge tutto come prima |
|
||||
|
Ma c’è un modo per capire quanti sono i termini da sommare senza contarli?
|
|||||
|
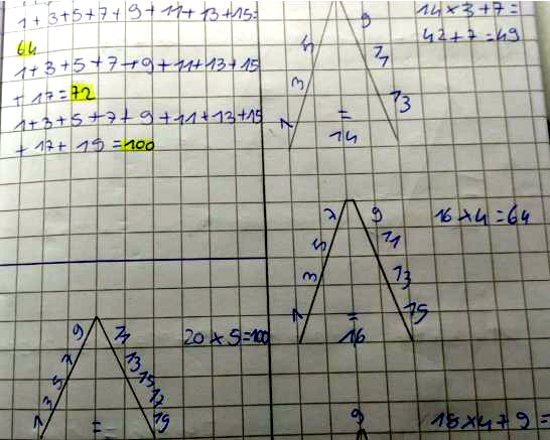
Dimostriamo che la somma di n numeri dispari consecutivi, a partire da 1, è il quadrato di n. |
|||||
|
Ora sommiamo i numeri dispari consecutivi... |

|
||||
|

|
||||
|
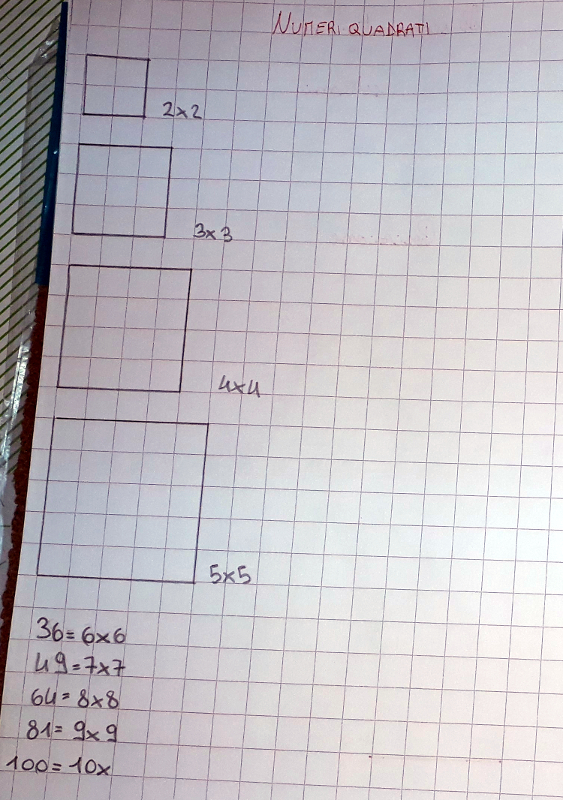
Siamo passati, quindi, a svolgere un'ulteriore attività, avendo a disposizione dei tappi di plastica, o dischi realizzati con del cartoncino. Viene richiesto di realizzare dei quadrati
specificando di non fare solo il contorno, usando il materiale a disposizione. Abbiamo parlato di quei numeri, chiamati “numeri quadrati” proprio perché in geometria
hanno la forma di un quadrato, che si ottiene moltiplicando un numero per sé stesso. |
|||||
|
|||||
|
Giunti a questo punto, chiedo ai miei alunni se, secondo loro sia possibile mostrare, con il loro materiale, che la somma dei dispari consecutivi è un quadrato, come abbiamo visto precedentemente sul tetto di Fibonacci.
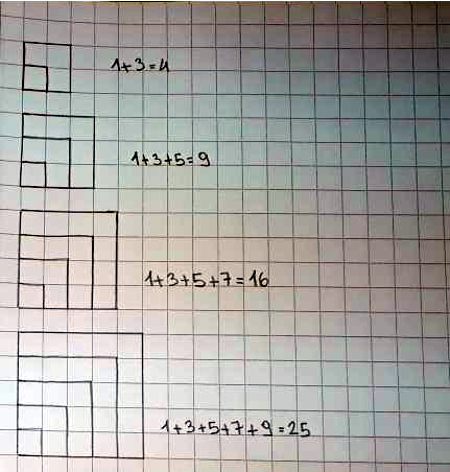
Procedono con tentativi fin quando un’alunna mi spiega che un tappo circondato da altri 3 ne fanno 4: il verbo “circondato” non è idoneo ma mi mostra con i suoi tappi quanto mi vuole dire. I 3 tappi sono disposti come uno gnomone, utilizzati per completare il numero presente per diventare un altro quadrato.

|
|||||
|
C’è chi preferisce, come prima, disegnare quanto svolto in maniera differente.
|
|||||
|
Mi è stata posta questa domanda: Gli alunni hanno compreso che la somma dei dispari consecutivi è un numero quadrato, sia dalla progressione disposta sul diagramma di Fibonacci, sia in geometria, sfruttando gli gnomoni. Erano anche sorpresi dal fatto che il 25 si ottiene sommando 5 dispari consecutivi, cioè che n2 = 1 + 3 + 5 +.... dove il numero degli addendi è proprio n. |
|||||
|
Esempi di problemi risolvibili con il diagramma di Fibonacci.
In questo anno scolastico è stato reintrodotto lo studio dell’educazione civica a scuola,materia che si tratta trasversalmente in tutte le discipline. Un obiettivo che è stato fissato per la matematica, e che è stato sempre una priorità (indipendentemente o meno dall’educazione civica!) è quello di mostrare come la matematica, mediante la schematizzazione, permetta di risolvere delle situazioni problematiche, quelle che da qualche anno sono le protagoniste dei cosiddetti “Compiti di realtà”. Con queste premesse, ho deciso di proporre ai miei alunni la lettura del problema XII.1.6 del Liber Abaci.

|
|||||
|
A lettura ultimata, gli alunni sono un po’ interdetti e mi dicono che vogliono verificare se è vero che i due viaggiatori si incontrano dopo 39 giorni. Dopo 39 giorni il primo avrà percorso 20x39 miglia, cioè 780. Il secondo invece devo calcolarlo con il tetto di Fibonacci: quindi faccio 39+1, cioè 40, lo moltiplico per 19 (che è la metà di 39, con resto) ed ottengo 760, a cui aggiungo la metà di 40, cioè 20, ed ho 780. E’ proprio lo stesso risultato, quindi si incontrano. Purtroppo, non ho potuto dedicare ulteriore tempo in classe, la campana suona sempre presto quando si lavora. Così ho chiesto di inventare un problema del genere a casa, cercando di schematizzare il numero di giorni e le distanze percorse da due uomini. 
Nel compito precedente, un'alunna con disturbi specifici dell'apprendimento ha inventato il seguente problema, scritto in maniera leggermente differente: Marta e Maria devono andare a scuola: Marta percorre 10 miglia al giorno, Maria 1 miglio in più del giorno precedente. Dopo quanti giorni si incontreranno a scuola? |
|||||
|
Il tetto di Fibonacci con Python Ho pensato di far programmare solo alcuni alunni su Python, cercando di creare un codice che permetta di eseguire la somma dei termini di una progressione conoscendo il primo e l’ultimo termine, la ragione della progressione (cioè di quanto aumenta l’addendo, secondo gli alunni) e il numero di termini da sommare. Questa attività è stato proposta in verticale in tutte le mie classi: in prima, in seconda ed in terza. Il “problema del tetto” è stato affrontato allo stesso modo, ovviamente i tempi sono stati più ristretti grazie al livello di preparazione dei ragazzi. |
|||||
|
Per la scrittura di tale programma occorre una conoscenza di base del software, cioè conoscere i comandi print, input, conoscere l’ordine delle operazioni da svolgere, l’uso delle parentesi e come sono considerati i numeri.
Per l’apprendimento dei comandi base ho caricato delle piccole video lezioni nella piattaforma scolastica, insieme a tutti i materiali che noi insegnanti mettiamo a disposizione. Prima di programmare, abbiamo analizzato quanto chiedere al software: sicuramente occorre inserire il primo e l’ultimo termine della progressione, nonché la ragione. Occorre anche calcolare il numero dei termini della progressione, oltre che la somma dei termini, ma, soprattutto, constatare se i dati inseriti sono quelli di una progressione. Ho mostrato agli alunni un mio diagramma di flusso ma li ho invitati a seguire anche un percorso differente, purché dia lo stesso risultato. |
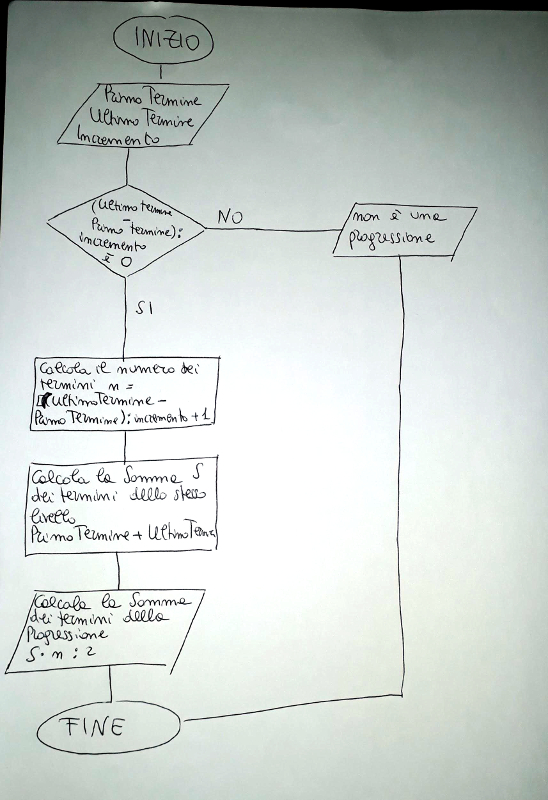
|
||||
|
Alcuni errori riscontrati sono dipesi dall’uso delle parentesi o delle formule, i comandi più “elaborati”, come if...else hanno destabilizzato gli alunni della classe prima, ma non gli altri. Qui di seguito è riportato il codice preparato da Chantal, un’alunna della classe seconda, seguendo un ordine differente da quanto mostrato nel diagramma di flusso in quanto ha seguito il proprio ragionamento. 
|
|||||
|
Chantal ha creato in modo corretto quelle che abbiamo chiamato “scatole”, cioè il
contenuto dell’input. 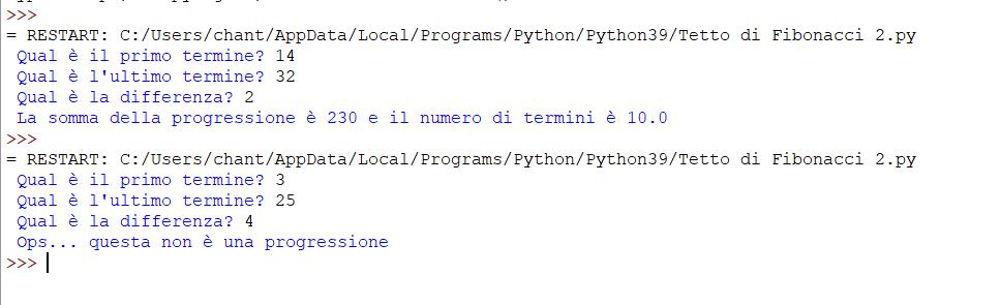
|
|||||
|
Nel seguente video, l’alunna spiega come ha realizzato il file. |
|||||
|
|
|||||
| | |||||