Fine primo anno della scuola secondaria, inizio del secondo. Si studiano le frazioni, seguite dai numeri decimali, segmento fondamentale nello studio dell'aritmetica.

Gli alunni conoscono le frazioni dalla scuola primaria, mi raccontano di quando la maestra le ha spiegate in classe portando delle barrette di cioccolato o delle pizze, che sono rimaste impresse nei loro ricordi, evidentemente l'insegnante li aveva presi per la gola. Mi fanno disegni per spiegarmi cosa significa ¾ o ⅕, e mi dicono che mangiare mezza pizza o 2/4 è la stessa cosa, anche se da questa affermazione qualcuno già perde l'entusiasmo con cui parlava prima di cibi divisi in parti uguali.

Quello che gli alunni cercano di descrivermi è il concetto di frazione come operatore, cioè legato all'operazione del dividere l'intero. Sanno calcolare i ¾ di 20, anche abbastanza velocemente ma non sanno che la frazione da sola rappresenta un numero, posto sulla retta orientata insieme agli interi. Questo sarà lo scopo delle mie lezioni, far comprendere che si tratta di numeri, chiamati razionali, oltre ad insegnare loro ad usarli nelle varie operazioni.

La didattica che porrò in atto per la comprensione delle frazioni ė ispirata a quanto descrive Leonardo Pisano Fibonacci nel Liber abaci, nel quale per la prima volta in Europa si trattano le frazioni come numeri e non solo come rapporto (come mostra Euclide nel quinto libro degli Elementi).

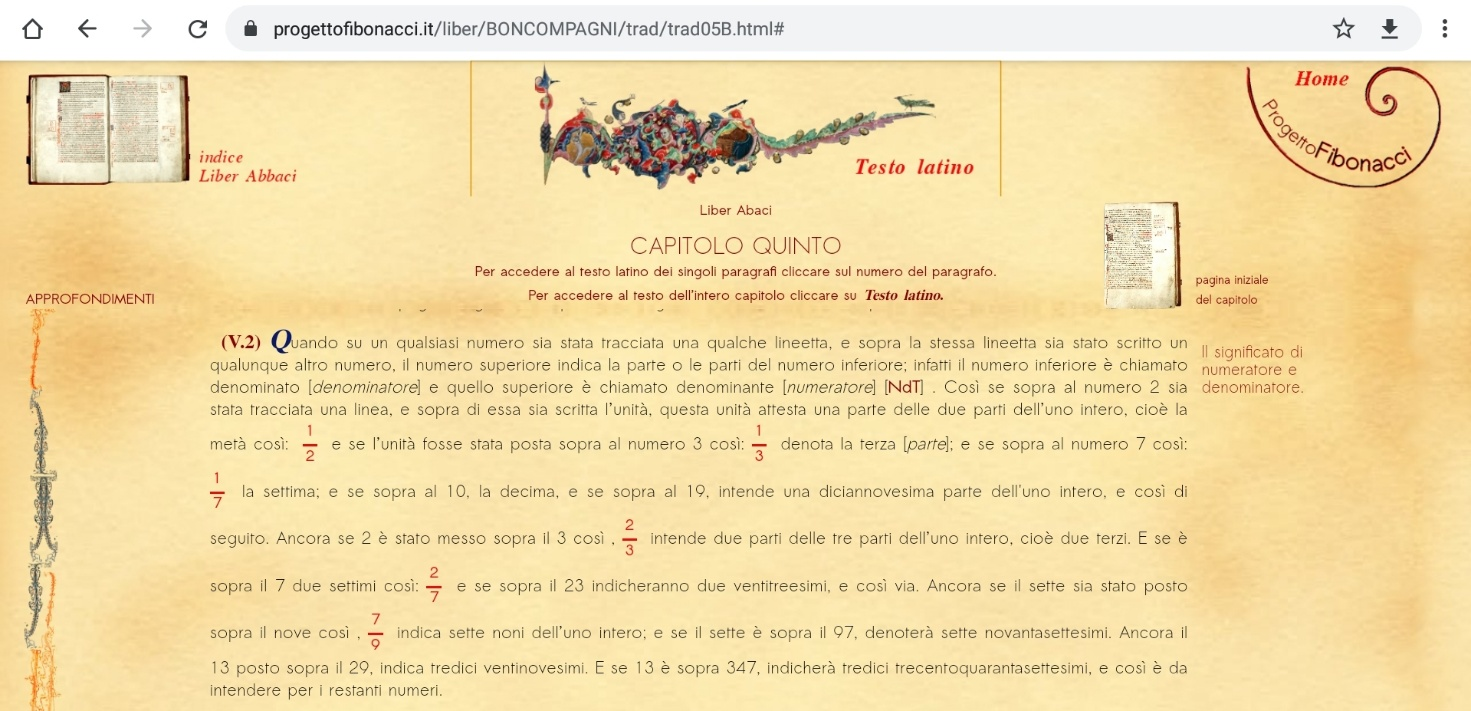
Dal sito www.progettofibonacci.it, considero la traduzione del quinto libro del Liber abaci.

Cominciamo a leggere la descrizione di un numero rotto, il denominante sulla lineetta, il denominato sotto, il secondo indica la suddivisione dell'intero, il primo le parti da considerare di tale suddivisione. Questa attività di lettura ha come scopo quello di mostrare una descrizione dettagliata di un argomento già visto, immergendolo però in un contesto storico,  usando termini diversi ( numero rotto, e non frazione propria, denominante e denominato, solo come sinonimi di numeratore e denominatore). Inoltre il mio scopo è anche quello di suscitare curiosità: se Fibonacci nel 1202 descrive i numeri rotti, come erano espresse prima le quantità più piccole di un intero?

Costruzione del materiale

Per definizione un numero rotto 1/n si ottiene dividendo l'intero in n parti uguali. 

Sappiamo dividere un segmento in parti uguali?

Alcuni rispondono negativamente, altri in modo affermativo, specificando però di saperlo fare solo per alcuni casi (se traccio l'asse del segmento divido in 2 parti uguali, se faccio la stessa cosa ad ognuno dei segmenti ne ottengo quattro, e così via), ovvero per un numero di parti uguali alle potenze di 2.

Propongo allora una costruzione geometrica che sfrutta il teorema di Talete per dividere un segmento in n parti uguali.

La costruzione geometrica ha come scopo quello di far comprendere la precisione della frazione a discapito delle misurazioni con il righello: in effetti, nel dividere in 3 parti un segmento di 10 cm con il righello "perderei" qualche millimetro, con la costruzione geometrica non accade. Questo discorso sorprende i ragazzi.

Presentazione del mio materiale.

Ho mostrato agli alunni i numeri rotti 1/n, per n che va da 1 a 10. L'intero ė stato realizzato con un'asta di legno da 10 cm, e tutti gli altri numeri come divisioni in n parti uguali. Il materiale è presentato dentro una scatola, ordinate in base ad n.

La manipolazione di oggetti nuovi e l'odore del legno stimola gli alunni a scrutare attentamente il materiale.

Prof, io vorrei costruirlo, dove si comprano le aste?

Posso usare un altro materiale?

Ho dato dei suggerimenti,  ho pregato precisione, ma ho dato anche materiale stampato da ritagliare e plastificare, ma quasi tutti hanno cercato di avere il materiale da cui si dovrà capire qualcosa d'importante in maniera solida.

Riduzione a numeri rotti più piccoli

Si considerano le aste o altro materiale alternativo. Chiedo di prendere il blocchetto da ½ e di fare in modo di formare altre "righe" con numeri rotti più piccoli. Si fanno diversi tentativi e si arriva a costruire un "muro" di numeri rotti che indicano la stessa quantità perché le righe hanno tutte la stessa lunghezza.  Il termine muro ė usato da alcuni alunni che mi riferiscono che tale procedimento ricorda loro quando usavano i regoli nella scuola primaria per imparare le prime somme, e scrivere in tutti i modi possibili un numero ( si parla delle partizioni dei numeri naturali). Si fanno altri esempi per permettere di capire il meccanismo che sta alla base della trasformazione, ma ė abbastanza immediato perché bisogna moltiplicare il denominante ed il denominato per lo stesso numero.

Per la riduzione ai numeri rotti più piccoli, gli alunni che non hanno a disposizione il materiale  si mostrano spaesati perché non hanno capito cosa fare. Si guardano intorno e sbirciano dai compagni dicendo di aver bisogno ancora di tempo. Quando qualcuno comincia a dire la regola, provano a dare i risultati degli esercizi dati, ma non di tutti. Alloro, metto a disposizione il mio e giungono presto alla regola.

Confronto tra numeri rotti

Ė più grande ⅚ o 4/9?

C'è chi risponde uno, chi l'altro. Non hanno idea di come fare, sanno che 1/9 è più piccolo di ⅙, ma poi non sanno come procedere, fin quando il più svogliato fa notare che hanno le aste. Costruiscono ⅚ prendendo 5 blocchetti da ⅙, 4/9 con 4 blocchetti da 1/9, ma li dispongono lontani.

Come decidete qual è il più grande?  Un'alunna risponde Come per i segmenti prof, dovrei usare il compasso. Allora suggerisco loro di mettere le file di mattoncini una sotto l'altra, anche con l'intero, e così giungono alla risposta.

Sono stati svolti diversi esercizi, conclusi tutti con un confronto empirico tra lunghezze. Qualche alunno si mostra un po' contrariato ad usare il materiale perché ritiene che sia abbastanza grande per capire senza giocare.  Ovviamente non insisto ma propongo  gli stessi esercizi senza il materiale: riescono a confrontare anche senza. È emersa, quindi,  per tutti, l'esigenza di estrapolare una regola per il confronto che andasse oltre la manipolazione delle aste. Ho chiesto ai ragazzi se riuscissero a schematizzare una regola. 

In primis, hanno posto il caso più semplice, ovvero due numeri multipli diversi dello stesso numero rotto: è maggiore quello con il denominante maggiore.

a/n e b/n, ovvero a×1/n e b×1/n. Per decidere il maggiore confronto a ed b.

Es. 5/7 e 3/7 sono entrambi multipli del numero rotto 1/7. Allora sarà maggiore 5/7.

Per seguire, se i numeri  multipli dei rotti sono tali che un rotto sia multiplo dell'altro, allora si scriverà in numeri rotti più piccoli il maggiore e ci ricondurremo al caso precedente. Utilizzando il linguaggio antico, si scrivono entrambi i numeri rotti in numeri simiglianti.

a/n e b/m, con m=kn. Allora scrivo in numeri rotti più piccoli a/n, e diviene ak/m. Ora si confrontano ak/m e b/m come nel caso precedente.

Es. ¾ e ⅝. Scrivo ¾ come 6/8 e confronto 6/8 con ⅝.

Infine, se i numeri multipli dei rotti non rientrano nei due casi precedenti, si cercherà il numero rotto più piccolo che divide entrambi i numeri presenti, e si procederà come nel caso precedente. 

a/n e b/m, con n e m non multipli. 1/n e 1/m possono essere scritti entrambi in numeri rotti più piccoli, secondo il numero rotto 1/s. ( ho indotto i ragazzi a capire cosa fosse il numero s)

Sia s=kn e s=hm, allora si ha a/ n = ka/s e b/m= hb/s, e si confrontano i denominanti.

Es.: ⅔ e ½. ⅓ e ½ contengono entrambi ⅙. Per cui, ⅔=4/6 e ½=3/6, e confronto come prima.

Questa schematizzazione, soprattutto l'ultimo caso, ci tornerà utile per effettuare la somma tra rotti.

I numeri misti

I numeri rotti possono trovarsi anche dopo l'uno?

Ovvio, perchė sappiamo che possiamo mangiare una pizza e mezza!

Comincio allora a classificare le frazioni come le intende Fibonacci in numeri rotti e misti: un numero misto ė formato dalla somma di un numero intero e di un numero rotto. Chiedo allora di formarne alcuni con il materiale a disposizione.

Un'alunna prende 2 interi e 2/5, chiedendomi se fosse quello un numero misto. Il mio annuire suscita curiosità poiché qualcuno mi dice di non aver mai visto in passato frazioni scritte in questo modo. I numeri rotti assomigliano alle frazioni proprie che già conosciamo, ma questi misti ricordano solo il modo che usiamo per leggere l'ora (sono le 9 e ¾) o le dosi di una ricetta (1 bicchiere e mezzo di latte).

I ragazzi hanno capito che si tratta di un modo differente di scrivere le frazioni più pratico e facile da capire. Chiedo ai ragazzi se mi definiscono una frazione “propria" e mi rispondono che sono come i numeri rotti di Fibonacci, cioè che sono divisioni in parti uguali di 1. Allora chiedo se hanno studiato un altro tipo di frazioni e mi parlano di quelle improprie, che hanno il numeratore maggiore del denominatore. Mi fanno degli esempi e chiedo loro di disegnarmele o di dirmi se sono un numero sulla retta dei numeri. Non mi sanno rispondere, a nessuna delle due richieste. Questo la dice lunga sulla loro comprensione del significato della frazione impropria, l'hanno studiata, ricordano la definizione ma non hanno capito cosa rappresenta. Fibonacci ci offre la possibilità di colmare questa mancata comprensione, l'uso del materiale agevola tutto. Chiedo agli alunni di sistemare le aste di 2 e 2/5 con soli numeri rotti: dentro un intero 5 blocchetti da 1/5, in due saranno 10 e con i 2/5 siamo a 12×1/5, cioè 12/5. Ecco la frazione impropria. Qualcuno ha un'espressione sul viso, come una illuminazione, e puntualizza che la frazione impropria è un numero misto, e viceversa. A tale affermazione decido di dir loro che dal punto di vista storico ci sono stati dapprima i numeri misti e dopo qualche secolo la classificazione delle frazioni che conoscono già. Ovviamente nasce una discussione su com'è meglio o peggio ma tutti sono convinti che il numero misto ė di più semplice comprensione. Si cominciano a trasformare numeri misti in frazioni improprie, come si può vedere dal video Da un numero misto a una frazione.

Chiedo, ora, di passare da una frazione impropria ad un numero misto. Considerano 7/3, prendono 7 blocchetti da 1/3 e poi sistemano sotto 2 interi ed 1/3. Svolgono bene le diverse trasformazioni richieste perché hanno a disposizione il materiale. Chiedo loro di trasformare 26/7, non hanno a disposizione 26 blocchetti da 1/7, cercano di unire il materiale didattico presente in aula ma si confondono perché differente. Sono quindi costretti a pensare una regola che li aiuti. Devo vedere quante volte il 7 sta nel 26, e rimane il resto. Questa ė la prima frase sensata che esce fuori dalle loro discussioni, per cui chiedo di spiegare meglio. Se faccio 26:7 ho il numero di interi, il resto sono i numeri rotti, ho anche controllato con gli esempi di prima. Quindi 26/7 è 3 e 5/7.

Dunque, se m>n, m/n= m:n+ r/n, ed è stato compreso in modo autonomo con esercizi basati sulla manipolazione concreta, e solo in seguito senza materiali.

video Da una frazione a un numero misto.

Somma di numeri rotti

Con la trattazione dei numeri misti, i ragazzi cominciano a capire che le frazioni sono numeri, nel nominarli come numeri rotti e numeri misti lo stanno già affermando. E se sono numeri, si possono fare tutte le operazioni. Si comincia con la somma di numeri rotti. Ispirandomi a quanto fatto nel Liber abaci da Fibonacci, comincio nel far fare le somme con le aste di cui disponiamo. Come hanno già appreso per il confronto, sanno sommare i numeri rotti con lo stesso denominato, per cui 2/5+1/5 =3/5. Quindi, se due rotti hanno lo stesso denominatore, la loro somma è la somma dei numeratori. Puntualizzo, però che ai tempi di Fibonacci non esistevano i simboli + e =, si mostrano sorpresi chiedendomi come riuscissero a fare allora le somme. Rispondo loro che il simbolo indica un'azione, per cui fare 3 e 5 o scrivere 3+5 significa fare l'unione di un insieme di 3 oggetti con uno di 5, e si avranno comunque 8 oggetti indipendentemente dal simbolo usato. Faccio notare, quindi che 2/5 e 1/5 sono 3/5, come lo avrebbero letto in passato.

Si passa, allora, a sommare due rotti, con un denominato multiplo dell'altro: ricordano che si scrive il numero rotto con denominato più grande in numeri rotti più piccoli, proprio i rotti dell'altro, tanto da renderli simiglianti e sommare così i numeratori. Quindi ½ e ¾ significa sommare 2/4 e ¾, cioè 5/4, che scritto in misti è 1 ¼.

Se, invece, i denominati non sono uno multiplo dell'altro , si cerca il numero rotto che divide entrambi e si rendono simiglianti come prima, sommando i denominanti.

Per il primo caso, i ragazzi non hanno usato il materiale, per il secondo solo alcuni lo hanno usato in quanto non è stata ben interiorizzata la regola che permette di scrivere un numero rotto in numeri rotti più piccoli e questa ė stata l'occasione per rivedere ciò che non ė stato ben compreso.

Per il terzo caso, invece, il materiale è stato usato da tutti, ovviamente sono state assegnate somme tra numeri rotti il cui denominatore della somma fosse al massimo 10. In questa occasione, mi sono resa conto che non tutti i ragazzi avevano ben chiaro il concetto di minimo comune multiplo. Cercare il numero rotto più piccolo che divide entrambi gli addendi significa cercare il mcm dei denominati perché non si possono sommare cose di diversa misura, serve una misura comune.

Durante le lezioni successive e come compito assegnato per casa, gli alunni svolgono un gran numero di somme affinché la ripetizione del procedimento vada a rafforzare l'apprendimento della regola. Per ora, sommano solo due addendi, ben presto si passerà ad un numero maggiore. Ognuno realizza sul proprio quaderno una tabella sulle somme dei numeri rotti con denominatori da 2 a 10, in ordine di assegnazione.

Si mostrano, infine, le tabelle delle somme dei numeri rotti presenti nel manoscritto del Liber abaci, custodito nella Biblioteca Nazionale di Firenze.

Le osserviamo insieme. La prima cosa che viene evidenziata, e che conferma quanto era stato detto, ė l'assenza dei simboli + e =. Si comprende che in rosso ci sono gli addendi ed in nero la somma, tranne in alcuni casi in cui ė sempre in rosso o il riquadro è vuoto. Ma osservando attentamente le figure usate, notano una discrepanza dalle figure indiane che conoscono. ( il 2, il 3, il 4 ed il 5 sono capovolti). Per fare chiarezza, leggiamo un estratto della scheda su Gerberto d'Aurillac di Maria Irene Guagnini presente nel sito www.progettofibonacci.it.

Gli alunni, che ben conoscono l'evoluzione dei sistemi numerici dal romano a quello decimale, comprendono l'esistenza di un abaco di “transizione" tra i due, dotato di 9 gettoni ( lo zero non era ancora contemplato) , erroneamente ruotati dai quali sono nati i simboli che usiamo. Mi piace raccontare gli aspetti storici ai miei alunni perché si mostrano sempre incuriositi da ciò che è accaduto nel passato e questo mi motiva a studiare le modalità con le quali impostare le mie lezioni e costruire la mia didattica. Questo mio pensiero mi spinge a mostrare loro le tabelle nel manoscritto, affinché venga compreso che qualcuno ha scritto un testo per spiegare delle grandi novità ad una moltitudine di gente, in qualche modo paragonabile a quello che io mi accingo a fare ogni giorno con loro. Proprio per questo chiedo ai miei alunni se vorrebbero realizzare una copia tutta loro delle tabelle e di averla in classe a disposizione per i loro conti. Sono ben disposti, anche a scrivere le parti che mancano e a scrivere alcuni risultati in forma diversa. Ognuno di loro effettuerà lo stesso numero di somme su un foglio da riportare, alla fine, su un gran cartellone, che, quindi, si formerà come un puzzle.

Si cerca quindi l'area che il cartellone deve avere. Si devono scrivere le somme su 12 fogli. Discutono su come calcolare l'area, sapendo che ciascun foglio ha le dimensioni di 30 e 21,2 cm. Qualcuno, dai risultati mi dice che non basta una parete, ha qualche problema con le equivalenze con le misure di superficie, le rivediamo insieme e si fanno gli opportuni conti.

Si passa a lavorare con la propria parte di somme da trascrivere, dopo averle controllate dal proprio quaderno.

Infine, si assemblano tutte le somme richieste, se ne correggono alcune, se ne aggiungono altre e con forbici, colla e pennarelli i ragazzi si mettono a lavoro per il loro cartellone. Sono soddisfatti del lavoro svolto, i loro visi sorridenti sono davvero motivanti.

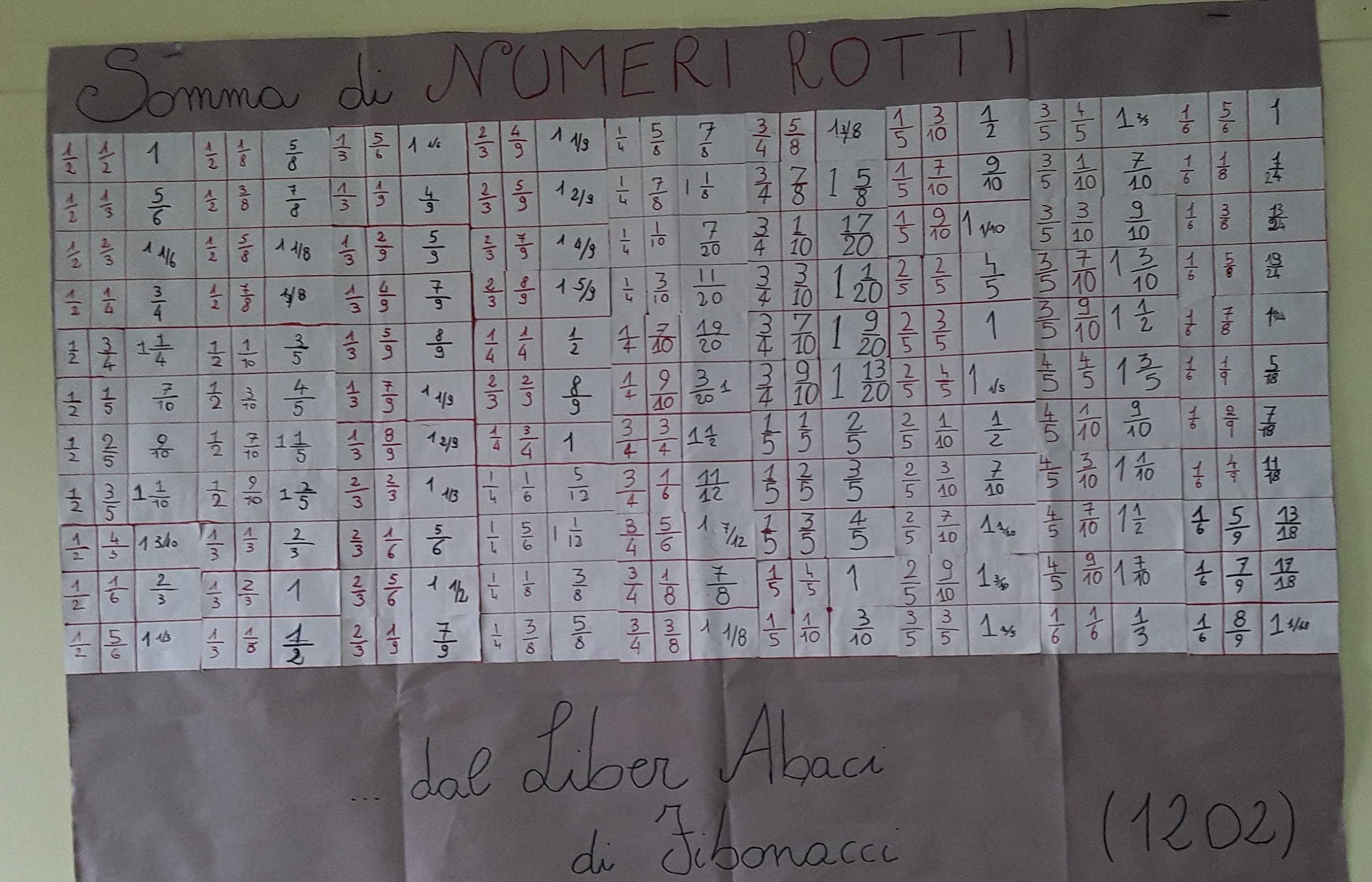
Nel video Somma di rotti.un esempio di calcolo della somma di rotti.

Somma tra numeri misti.

Fibonacci parla dei numeri rotti e dei misti. Vediamo ora come sommare i misti.

Proviamo a sommare 1 ¼ e 2 1/8. Non è difficile dedurre la regola ma qualcuno di loro mi dice che sembra troppo semplice: i ragazzi mi dicono che si opera sempre con lo stesso principio, cioè rendere tutto simile, per cui si raggruppano i numeri in base a similitudini, cioè gli interi con interi e i rotti con i rotti. Così dicendo dicono che il risultato è maggiore di 3, per essere precisi ¼+1/8 dopo 3, ovvero 3 3/8. Per verificare la correttezza del conto controllano le lunghezze delle due file di aste come sempre.

Mostro anche il metodo di somma tra misti che prevede la trasformazione dal numero misto a frazione impropria, si rendono le frazioni simiglianti e si sommano come i rotti. Infine, se si vuole, si riporta come numero misto.

I ragazzi preferiscono il primo metodo perché quello appena mostrato ė più lungo!

in realtà, penso che la loro “contrarietà” a questo secondo metodo dipenda dal fatto che non vogliono avere due strategie risolutive ma solo una...tanto che dicono di usare il primo metodo per non sbagliare, perché sembra loro più intuitivo.

Sono state, poi, assegnate somme con un numero di addendi maggiore o uguale a tre, dapprima solo con numeri rotti, poi anche con numeri misti, per mia scelta scritti come frazione impropria, per vedere come si sarebbero comportati nel trovarseli lì, tra i conti. Ebbene, nel guardare i vari addendi, hanno riconosciuto la frazione impropria, traducendola come somma di un intero ed un rotto, ma hanno poi compreso che la scrittura in frazione impropria in questo caso li avrebbe aiutati nei conti. Quindi hanno ridotto in numeri simiglianti e sommato i numeratori.

Differenza tra numeri rotti.

Ora vedremo come fare la differenza tra rotti.

Cosa potrà mai starci di diverso?

Gli alunni pensano che non sia molto diverso il procedimento nel fare la differenza tra rotti perché si dovrà cercare di rendere simiglianti i numeri e sottrarli anziché sommarli.

Non è errata la loro intuizione, per cui assegno loro una sottrazione tra rotti, e, senza alcuna difficoltà la eseguono.

Allora pongo loro il seguente problema.

Cerca quel numero che sommato ad 1/5 mi dia 7/10.

Mi guardano perplessi, non sanno cosa scrivere e come procedere. Mi dicono che non capiscono la richiesta del mio problema. Allora penso a formularlo con i numeri naturali.

Cerca quel numero che sommato a 5 mi dia 15.

è il 10!

Li invito a riflettere sulla risposta che mi è stata data, ovviamente corretta e mi fanno notare che è un modo diverso di chiedere di fare una differenza, quindi 5+”cosa”=15, cioè 15-5=”cosa”, cioè 10.

Metto a disposizione le aste e chiedo di sistemarle per capire dove posizionare la “cosa”.

Allora considerano nuovamente i numeri rotti. ⅕+”cosa”=7/10, cioè 7/10-⅕=”cosa”. Riducono in numeri simiglianti e vedono che la “cosa” vale ½, e lo verificano con la rispettiva asta.

Prendono appunti sui loro quaderni, per ricordare meglio...

Nel video Differenza tra rotti.un esempio di utilizzo del cartellone per la differenza

Presentare la sottrazione ponendo un problema simile a quello dato ha creato difficoltà perché tale operazione era presentata come l’inversa dell’addizione e gli alunni, invece, non ne hanno tenuto conto. Solo dopo un’attenta riflessione hanno compreso la richiesta del calcolo della differenza formulata in modo diverso.

Sempre meglio far riflettere, dalle difficoltà nasce sempre un nuovo apprendimento!