La disgregazione e le frazioni egizie
Scomposizione di una frazione in frazioni unitarie.

Laura Tomassi

Nella classe 2B2 abbiamo intrapreso un percorso cominciato con il racconto del mito di Horus e proseguito con un problema di disgregazione di una frazione propria in frazioni unitarie. La fonte bibliografica di tale idea è stata la lettura della scheda "La disgregazione:scomposizione di una frazione (propria) in frazioni unitarie" Franco Ghione, e la motivazione che mi ha spinto a fare questo percorso con la classe è di molteplice natura: innanzitutto mi permette interdisciplinarietà, poi di approfondire problematiche riguardanti l’algoritmo della somma di frazioni, guardandolo da un punto di vista inverso, quindi assolutamente formativo; in ultimo soddisfa pienamente la modalità di lavoro laboratoriale che questa classe ha fortemente ostacolato all’inizio del suo cammino insieme a me, ma al quale ora con grande profitto e soddisfazione si dedica.

D’altra parte la motivazione che Fibonacci adduce per lo studio della disgregazione mi sembra più che convincente per metterci su questo cammino.

Divisi in coppie, i ragazzi hanno affrontato il seguente problema: dividere cinque quadrati in maniera da avere sei parti uguali.
Il problema è stato affrontato dapprima "con le mani" e poi "con la mente"

 "con le mani":
Dovevano dividere cinque quadrati ( realizzati da loro con costruzione riga e compasso e ritagliati) per sei di loro ( i sei ragazzi ospiti di un’altra classe) in maniera da avere sei parti uguali.
Si è aperta una discussione su come poter fare. Il grande successo è stato che uno degli alunni ospiti per caso nella nostra classe si è unito a noi nella soluzione del problema. Siamo arrivati a dire che si può risolvere il problema in due modi.
Negli elaborati i ragazzi scrivono qual è la frazione che ciascuno si ritrova in mano dopo aver fatto le divisioni. Vedono che in entrambi i casi la frazione totale è i 5/6, però nel secondo caso corrisponde alla somma di due frazioni con numeratore 1; mentre nel primo caso ad una somma di cinque frazioni con numeratore 1.
Inoltre i tagli da effettuare per risolvere il problema sono 7 contro 25: una disgregazione "migliore" delle due frazioni risulta essere la seconda? Loro dicono che concettualmente è più difficile ma nella pratica è più semplice. In queste immagini i loro quadrati ritagliati ed attaccati su un foglio, evidenziando le parti che toccano ad ognuno.

Questa divisione è stata simulata anche con la divisione in parti uguali di 5 mele per 6 ragazzi, come illustra questo video.


 "con la mente":
Li ho fatti riflettere sul fatto che il problema di dividere i quadrati in questa maniera corrisponde al problema di scrivere una frazione come somma di frazioni unitarie ( come possono notare se vanno a considerare la parte data ad ognuno) e spiegato che si tratta di un problema egiziano trattato nel papiro di Rhind e ripreso trattato nel Liber abaci da Fibonacci.
I ragazzi mi hanno fatto notare che secondo loro mi stavo contraddicendo: perché mai gli Egiziani avrebbero dovuto scrivere una frazione come somma di frazioni unitarie se conoscevano solo frazioni unitarie, come io più volte ho fatto notare?
Ho spiegato allora che
3
5 =
1
2 +
1
10veniva espresso tramite esempi concreti: ad esempio tre pani da dividere tra 5 operai e che anche le divisioni venivano fatte sfruttando le frazioni unitarie (ad esempio 13 : 8 = 1 +
1
2 +
1
8).

 Caso
a + b
a × b
Ho chiesto di guardare meglio la "struttura della frazione" che abbiamo considerato: abbiamo notato che il numeratore è la somma di 2 e 3 ed il denominatore il prodotto di 2 per 3; abbiamo poi affrontato il problema se ogni volta che si presentano frazioni con questa caratteristica [cioè
a + b
a × b] si può fare in maniera analoga. Ho chiesto loro di "inventare frazioni con questa caratteristica". I loro esempi sono riportati qui sotto.

Una considerazione importante che hanno fatto è che questo è il "contrario" di quando "abbiamo fatto la somma con denominatori diversi ma primi tra loro".
Soprattutto ci siamo resi conto che il problema di dividere un certo numero di quadrati per un certo numero di persone è risultato sempre corrispondente proprio al problema di scrivere una frazione in somma di frazioni unitarie.
La loro impressione è che però "sembrano due problemi proprio tanto diversi": questo perché fa parte della tematica generale importantissima dell’individuare la struttura base di un problema matematico e far emergere delle vere strategie risolutive dal magma indistinto che gli algoritmi, imparati inconsapevolmente e spesso alla rinfusa, rappresentano.

 Frazioni del tipo
a
b   con  b+1 = na    caso a=2

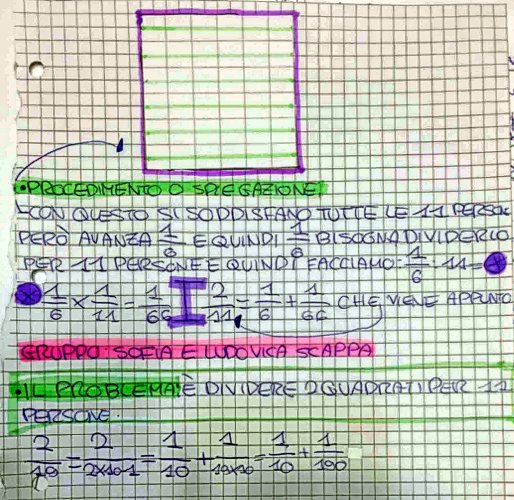
Abbiamo provato a ragionare con frazioni che hanno una struttura diversa: chiaramente io sono interessata al fatto che ragazzini di dodici anni siano attenti ad una struttura, un tipo: la formula deve diventare una descrizione sintetica di un caso ben delineato nella mente e perdere la sola funzione di ancora mentale per ricordare.
Abbiamo studiato un‘altra frazione proposta da Fibonacci nel Liber abaci: il caso
2
11.

Abbiamo posto come obiettivo che le disgregazioni che cerchiamo diano frazioni con denominatore diverso altrimenti si ottiene banalmente
2
n =
1
n +
1
n ( nel presente così come in tutti gli altri casi).

Lo hanno trattato come il caso precedente: dividendo 2 quadrati (questa volta quadrati non costruiti da loro ma ritagliati da fogli quadrettati per brevità), però la consegna prevedeva che si facesse la prima porzione più grande possibile.
Hanno diviso in sei parti e dato ogni sesto ad 11 di loro; poi il rimanente sesto è stato suddiviso in 11 parti, quindi un
1
66 di ogni quadrato.
Naturalmente qui si è posto l’accento sul fatto che fare
1
11 di
1
6 vuol dire sul foglio fare una moltiplicazione.
Ancora una volta il problema di scrivere la nostra frazione come somma di frazioni unitarie poteva essere rappresentato con il quesito della divisione dei quadrati.

Abbiamo cercato anche di dare una motivazione a questa divisione ed i ragazzi hanno immaginato che potesse corrispondere a frazionare per esempio il raccolto tra un certo numero di contadini disponendo di sacchi uguali: è chiaro che cerco di fare meno operazioni possibili muovendomi prima su frazionamento "grosso" poi sulla suddivisione del restante.

Si sono accorti che
2
11,
2
19,
2
5 ... tutte le frazioni con numeratore 2 e denominatore dispari possono osservare lo stesso criterio:

2
2× - 1 =
1
 +
1
((2× - 1) × )

Il fiore rappresenta n, un numero intero qualsiasi: ai loro occhi scrivere una formula con un simbolo grafico o letterale fa ancora differenza.

Qui è riportato uno degli elaborati dei ragazzi.



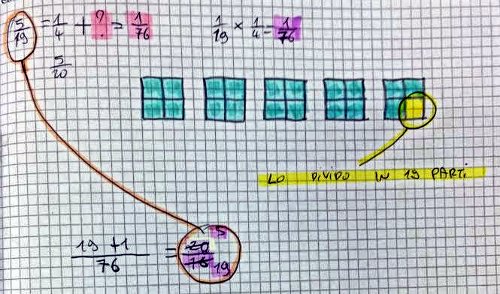
Ho posto loro la domanda se questo tipo di disgregazione e questa formula vanno bene anche quando il numeratore è diverso da 2.



 Per numeratore diverso da 2:   
5
19

Il proseguimento di questa idea è nella decomposizione delle frazioni in frazioni unitarie in generale.
All’età dei miei studenti, più che scrivere l’algoritmo generale è utile andare a leggere e capire insieme ciò che Fibonacci scrive a proposito del "settimo caso", ossia le frazioni che non possono essere fatte rientrare in nessuno dei sei casi che egli prende in considerazione. Ciò che scrive mi sembra davvero istruttivo e bellissimo nello stile:


Ci siamo occupati in particolare di andare a capire come fare con
4
13 e abbiamo fatto la considerazione che è più grande di
1
4 e più piccola di
1
3 e quindi si può scrivere
4
13 =
1
4 +

Il fiore ora rappresenta l’incognita, "la cosa", come l’abbiamo chiamata introducendo il linguaggio che Fibonacci riserverà all’algebra .
Per trovare la cosa abbiamo posto

=
4
13 -
1
4 =
16
52 -
13
52 =
1
52 +
2
52 =
1
52 +
1
26

A questo punto ho fatto sperimentare ai ragazzi l’utilizzo dell’algoritmo di Python, come inserito in link sulla pagina https://www.progettofibonacci.it/liber/BONCOMPAGNI/trad/trad07B.html


La loro conclusione è ……… che vogliono imparare come si fa a crearlo: mi sembra un ottimo punto di vista! Magari per obiettivi più semplici, ma troveremo il modo.


  L’occhio di Horus


La parte del percorso che ha stupito di più i ragazzi: il racconto del mito di Horus. Questo ha dato alla nostra matematica un taglio non solo storico ma anche emozionale e narrativo. Abbiamo scelto, tra le tante versioni esistenti di questo mito, quella riportata in D’Amore " La matematica dappertutto".

“Un pastore e la sua avvenente promessa sposa, sorvegliavano ciascuno il proprio gregge, distanti, quando un non ben precisato dio egizio, invaghitosi di lei, le apparve al tramonto chiedendole di passare la notte insieme; infuriatosi per l’inatteso rifiuto, il dio volò dal pastore e lo punì, strappandogli l’occhio e disperdendone nel deserto prima la metà, poi la metà della metà rimasta e così via per sei volte. Nel frattempo la fanciulla era corsa a cercare di salvare l’amato dalla vendetta del dio; giunse e, vista la scena, accettò di appartarsi la notte con il dio, pur di salvare il giovane. La mattina dopo, la promessa sposa tornò e, con amore infinito, ricompose l’occhio del malcapitato futuro sposo, rimettendo a posto prima la metà poi il quarto, poi l’ottavo, il sedicesimo, il trentaduesimo, il sessantaquattresimo dell’occhio. Il pastore riprese la vista e….”

L’immagine tratta dal loro quaderno è esplicativa di come ne abbiamo parlato.

Si è trattato di uno spunto riflessivo sulla somma delle frazioni della serie ⎧⎩
1
2⎫⎭n, il taglio narrativo era in realtà una strategia didattica. Dopo aver raccontato la storia abbiamo fatto delle piccole riflessioni.
Le loro osservazioni
  • "le frazioni esistevano quindi già molto prima di Fibonacci visto che il mito è ambientato nell’antico Egitto, ma allora professoressa c’è qualcosa che non torna con ciò che ci ha raccontato" ……
    "è un conto dire che le frazioni esistevano come concetto, è un conto dire che siano veri e propri numeri con una loro aritmetica no?"

  • "questo simbolo è un simbolo sacro…. Non è strano che racchiuda le frazioni?"
    "Professoressa,magari per loro la matematica rappresentava la perfezione degli dei"

  • "avete notato che le frazioni della storia di Horus hanno tutte numeratore uguale ad uno? Sono queste le frazioni Egizie"

  • Ma forse la domanda più interessante è "secondo voi ragazzi, quando la pastorella va a ricomporre l’occhio spezzato in 2, poi in quattro fino a al pezzo più piccolo (
    1
    64    ) ottiene di nuovo l’occhio intero?    "
    La risposta data da loro è nel calcolo della somma che ritroviamo sul quaderno…. ma io li ho portati a riflettere sul fatto che nel racconto quella frazione rappresentava un numero piccolo che per gli Egiziani poteva essere considerato infinitamente piccolo….. ma veramente è così?
    E così, forse in maniera un pò prematura, siamo passati a considerare e rappresentarci mentalmente la somma della serie ⎧⎩
    1
    2    ⎫⎭n per n "infinitamente" grande.
    Abbiamo cercato un materiale che fosse rappresentativo di come varia la frazione al crescere di n.
    Ho pensato di utilizzare il materiale di cartoncino laserato colorato che vedesse il quadrato unitario di lato 15 ( non è un caso …è lo stesso con cui abbiamo realizzato le moltiplicazioni e lo studio delle espressioni): questo materiale (di ispirazione montessoriana) è funzionale anche al discorso che faremo a breve sul teorema di Pitagora….. ci tornerà utile anche in seguito.
    I quadrati che rappresentano i termini della serie sono via via la metà l’uno dell’altro ma per disporli in maniera funzionale li ho dati come somma di quattro triangoli rettangoli isosceli .


Cerchiamo di visualizzare la somma per capire cosa succede quando le frazioni hanno via via denominatore più grande e quindi diventano infinitamente piccole. Attraverso una dimostrazione percettiva, abbiamo osservato che la somma converge a 1.
La frazione
1
2 		La frazione
1
4


La somma
1
2 +
1
4

La visualizzazione del risultato
1
2 +
1
4 =
3
4



La loro osservazione è stata però che è normale che se aggiungo infiniti pezzetti, alla fine ricomporrò l’intero perché "il buco centrale alla fine si ridurrà ad un punto", quindi per n infinitamente grande la somma di tutte le frazioni coprirà tutta l’area unitaria.
Sicuramente non è una dimostrazione in senso rigoroso ma prepara la mente e l’occhio a molte domande.

Ho deciso di mettere in crisi la loro osservazione “che è scontato che la somma di infiniti pezzetti pure se piccolissimi alla fine darà l’unità” andando a guardare un ‘altra serie: ⎧⎩
1
4⎫⎭n.
Abbiamo studiato la somma utilizzando un materiale simile al precedente: quadrati di cartoncino tagliato al laser. Ogni cartoncino è
1
4 del precedente, il cartoncino grande rappresenta l’unità.

⎧⎩
1
4⎫⎭n

Come spiegazione qui a fianco l’elaborato dei ragazzi, che è stato fatto come lavoro di gruppo , mentre la riflessione e verbalizzazione è stato dato come compito per casa.

Si sono convinti che la somma della serie è
1
3osservando che
1 = 3 × 
1
4  + 3 × 
1
42 + 3 × 
1
43 + 3 ×
1
44 + 3 × ... = 3 × ⎧⎩
1
4  +
1
42 +
1
43 +
1
44 + ...⎫⎭ = 1

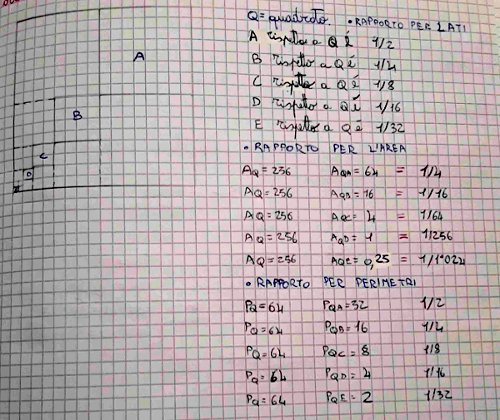
e che come dicono loro non tutte le somme portano a riempire l’unità.

L’elaborazione personale dei ragazzi è la parte più importante: riesce a guidarmi verso una fiducia maggiore nelle loro capacità ed evidenzia dei dubbi e delle certezze sbagliate, da mettere in crisi , come questa di Angela che afferma che il quadrato che ha area metà ha anche lato metà di quello precedente.

ll lavoro sulla somma delle frazioni unitarie ha introdotto il discorso del rapporto tra aree di figure i cui lati hanno un determinato rapporto.

Notevole è la frase di Angela, la quale dice “Il continuo dell’occhio di Horus….per sbaglio nella parte di geometria”… questo suo “sbaglio” non è casuale: i miei studenti non hanno più come dicevano all’inizio della prima “un quaderno di matematica ed uno di geometria”….
Mi sembra un obiettivo raggiunto molto importante.